- 1 Introduction
- 2 Getting Started with the Vehicle Specification Language
- 3 Proving Neural Network
Robustness
- 3.1 Neural Network Robustness as a Verification Property
- 3.2 Formalising \epsilon-ball robustness for MNIST networks in Vehicle
- 3.3 Definition of Robustness with Respect to a Dataset
- 3.4 Running the Verification Query
- 3.5 Exercises
- 3.5.1 Exercise (*): Run the Chapter code
- 3.5.2 Exercise (*) : Experimenting with \epsilon-balls of different size
- 3.5.3 Exercise (**) : Getting a statistical evaluation of robustness with respect to the given data set, for various \epsilons
- 3.5.4 Exercise (*) : Strong Classification Robustness in Vehicle
- 3.5.5 Exercise (**): Explore Other Definitions of Robustness
- 3.5.6 Exercise (**): Other Distances in Vehicle
- 3.5.7 Exercise (*) Practicing to write property specifications
- 3.5.8 Exercise (***): Conduct a complete “training - verification” experiment from start to finish
- 4 Property-Driven Training
- 5 Exporting to Agda
- 6 Conclusions and Future Directions
- References
1 Introduction
Welcome to the Vehicle tutorial page! In this tutorial, you will learn about neural network verification with Vehicle. Vehicle’s complete documentation and installation instructions are available on the vehicle documentation page.
The present tutorial contains contributions by:
- Matthew Daggitt
- Wen Kokke
- Ekaterina Komendantskaya
- Bob Atkey
- Luca Arnaboldi
- Natalia Slusarz
- Marco Casadio
- Ben Coke
- Jeonghyeon Lee
This tutorial has been run live and adapted for different audiences at:
FOMLAS’23 the 6th Workshop on Formal Methods for ML-Enabled Autonomous Systems co-allocated with CAV’23 in Paris, France; 18 July 2023;
VETSS Summer School at the University of Surrey, UK; 23 August 2023; Youtube recording available;
ICFP’23 the International Conference on Functional Programming in Seattle, USA; 08 September 2023.
We thank all our readers and attendees for their feedback and contribution. This FOMLAS’23 tutorial outline gives a summary of all tutorial resorces. To cite Vehicle tutorial, please use:
@inproceedings{FoMLAS2023:Vehicle_Tutorial_Neural_Network,
author = {Matthew Daggitt and Wen Kokke and Ekaterina Komendantskaya and Robert Atkey and Luca Arnaboldi and Natalia Slusarz and Marco Casadio and Ben Coke and Jeonghyeon Lee},
title = {The Vehicle Tutorial: Neural Network Verification with Vehicle},
booktitle = {Proceedings of the 6th Workshop on Formal Methods for ML-Enabled Autonomous Systems},
editor = {Nina Narodytska and Guy Amir and Guy Katz and Omri Isac},
series = {Kalpa Publications in Computing},
volume = {16},
pages = {1--5},
year = {2023},
publisher = {EasyChair},
bibsource = {EasyChair, https://easychair.org},
issn = {2515-1762},
url = {https://easychair.org/publications/paper/Rkrv},
doi = {10.29007/5s2x}}If you have any questions about the Vehicle tutorial, you are invited to join this Slack Channel for questions and discussions.
We hope you enjoy this course!
1.1 What is Neural Network Verification?
Neural networks are widely used in the field of machine learning; and
are often embedded as pattern-recognition or signal
processing components into complex software. Below we see a
schematic depiction of a neural network trained to classify hand-written
digits: 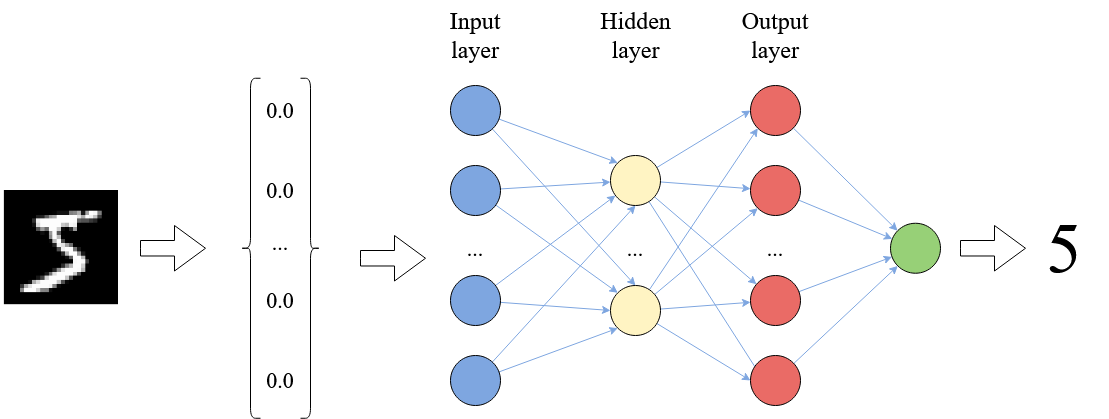
The image is represented as a vector of real numbers, each vector element standing for a pixel value. Each arrow in the picture bears a weight that is used to multiply the input signal; each neuron computes the sum of its inputs.
In some scenarios, it becomes important to establish formal guarantees about neural network behaviour. One of the first known attempts to verify neural networks, by (Pulina and Tacchella 2010), was based on abstract interpretation. The famous paper by Szegedy (Szegedy et al. 2013) that highlighted the problem of neural network vulnerability to small-norm input perturbations (“adversarial attacks”) gave additional impulse to this line of research. In CAV’2017, two papers, by Huang et al (Huang et al. 2017) and Katz et al. (Katz et al. 2017), on neural network verification appeared and both used specialised forms of SMT-solving. The later gave rise to Marabou (Katz et al. 2019), – a rapidly developing sound and complete neural network verifer, which we use in Vehicle.
In 2019, the ERAN verifier by Dingh et al. (Singh et al. 2019) appeared in POPL, and showed that performance of abstract interpretation methods compares favourably against those based on SMT solving. However, the range of properties they handled was limited to proving adversarial robustness of neural networks; moreover ERAN was incomplete. This line of research led to many subsequent extensions, e.g. by Muller et al. (Müller et al. 2022), (Müller et al. 2023) to mention a few.
Mixed Integer Linear Programming (MILP) methods were brought into this community by Bastani et al. (Bastani et al. 2016), and were further developed into working tools, e.g. Venus (Botoeva et al. 2020).
Neural network verifier extensions followed two main directions:
- scaling to larger networks (we can mention \alpha\beta-Crown (Wang et al. 2021) and GCP-Crown (Zhang et al. 2022) as VNN-COMP winners in 2021 and 2022);
and
- extending from piece-wise linear to non-linear activation functions. (An example are sigmoid neurons handled by Verisig using interval arithmetic (Ivanov et al. 2019).)
At the time of writing, there exist over a hundred verifiers for neural networks. Several papers and monographs are dedicated to the survey of the landscape, see for example (Liu et al. 2021), (Albarghouthi 2021), (Huang et al. 2020). The community established the specification standards VNNLib, common benchmarks and annual competitions. Vehicle compiles down to the VNNLib standard, with a view to be compatible with the growing family of verifiers.
Formally, a neural network is a function N : R^m \rightarrow R^n. Verification of such functions most commonly boils down to specifying admissible intervals for the function’s output given an interval for its inputs. For example, one can specify a set of inputs to belong to an \epsilon- neighborhood of some given input \mathbf{x}, and verify that for such inputs, the outputs of N will be in \delta distance to N(\mathbf{x}). This property is often called \epsilon-ball robustness (or just robustness), as it proves the network’s output is robust (does not change drastically) in the neighborhood of certain inputs.
Seen as functions, neural networks have particular features that play an important role in their verification:
- these functions are not written manually, but generated (or fitted) to model the unknown data distribution;
- the “data” may be big, and require large neural networks;
- we often attribute very little semantic meaning to the resulting function.
1.2 Challenges in Neural Network Verification
There are several research challenges in the area of neural network verification:
Theory: finding appropriate verification properties. The scope of neural network properties available in the literature is limited. Robustness is the most popular general property to date (Casadio et al. 2021), and others include mostly domain-specific properties, such as ACAS Xu Benchmark (Katz et al. 2017), which we will consider shortly in this tutorial. What neural network properties we want and can realistically verify still stands as a big research question.
Solvers: undecidability of non-linear real arithmetic and scalability of neural network verifiers. On the solver side, undecidability of non-linear real arithmetic (Akbarpour and Paulson 2009) and scalability of neural network verifiers [wang2021beta] stand as two main challenges.
Machine Learning: understanding and integrating property-driven training. In all realistic scenarios, even accurate neural networks require extra “property-driven training” in order to comply with verification properties in question. This requires new methods of integrating training with verification. Several approaches exist, including the recently introduced method of “differentiable logics” that translate logical properties into loss functions. But they all have pitfalls, see (Slusarz et al. 2023) for a discussion.
Programming: finding the right languages to support these developments Many existing solvers have low-level syntax that is hard to understand, making maintenance of the specification difficult. There is very little programming infrastructure to interface verification and property-driven training. Furthermore, the available language infrastructure only allows specifications to be written in terms of the input space, whereas one often needs to reason about neural network behavior in terms of the problem space. This creates an additional embedding gap on verification side, – a problem that eventually needs to be resolved.
Complex systems: integration of neural net verification into complex systems. Finally, neural networks usually work as components of complex systems, and the question of smooth integation of existing neural network solvers with other theorem provers requires resolution.
This tutorial will focus on problems 3 – 5, and will present Vehicle, a tool that provides support in alleviating them. In particular, Vehicle is equipped with a specification language that allows one to express neural network properties in a high-level, human-readable format (thus opening the way to reasoning about a wider space of properties, and reasoning in terms of the problem space). Then it compiles the specification down into low-level queries and passes them automatically to existing neural network solvers. If the specification cannot be verified, Vehicle gives one an option to automatically generate a new loss function that can be used to train the model to satisfy the stated property. Once a specification has been verified (possibly after property-driven re-training), Vehicle allows one to export the proof to an interactive theorem prover, and reason about the behavior of the complex system that embeds the machine learning model.
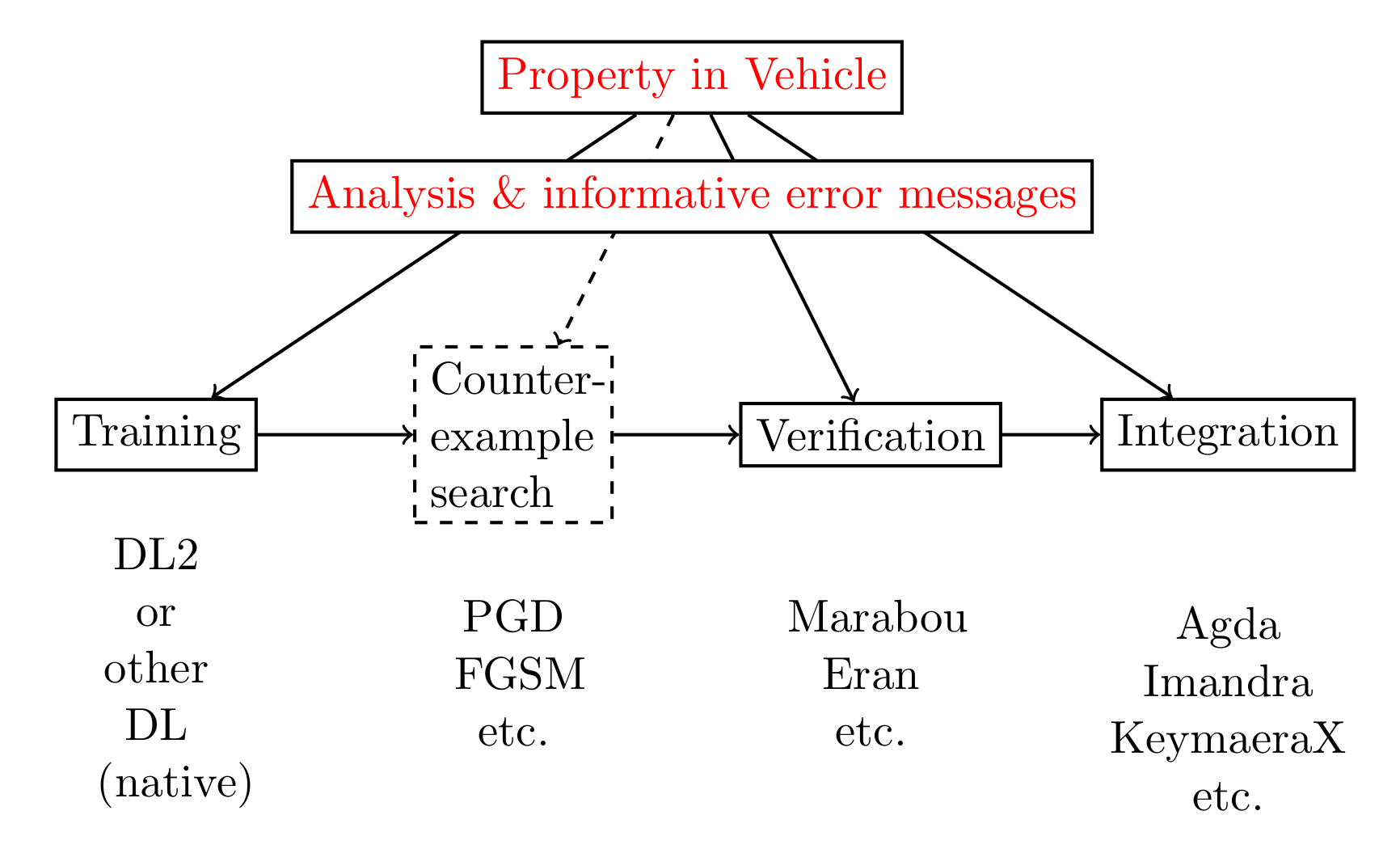
Vehicle programs can be compiled to an unusually broad set of backends, including:
loss functions for Tensorflow which can be used to guide both specification-directed training and gradient-based counter-example search.
queries for the Marabou neural network verifier, which can be used to formally prove that the network obeys the specification.
Agda specifications, which are tightly coupled to the original network and verification result, in order to scalably and maintainably construct larger proofs about machine learning-enhanced systems.
Currently, Vehicle supports the verifier Marabou, the ITP Agda, and the ONNX format for neural networks. The below figure illustrates the existing user backends in Vehicle.
1.3 Objectives of this Tutorial
This tutorial will give an introduction to the Vehicle tool (https://github.com/vehicle-lang/vehicle) and its conceptual approach to modelling specifications for machine learning systems via functional programming. It will teach the participants to understand the range of problems that arise in neural network property specification, verification and training, and will give hands-on experience at solving these problems at a level of a higher-order specification language with dependent types.
1.4 Prerequisites
To follow the tutorial, you will need Vehicle, Marabou and Agda installed in your machine. For instructions, refer to vehicle documentation.
Quick installation instructions:
For Chapters 1, 2 and 3 you only need to
Install Vehicle : just run
pip install vehicle-langInstall Marabou: just run
pip install maraboupy
Python (Tensorflow) and Agda installation will only be needed to follow Chapters 4 and 5.
We suggest that you start this tutorial with just Vehicle and Marabou as tools.
We recommend using Visual Studio Code with the Vehicle Syntax Highlighting and agda-mode plugins.
Whether you are using this tutorial for self-study or attending one of our live tutorials, all supporting exercises, code and infrastructure can be downloaded from the tutorial repository. These include all relevant property specifications, trained neural networks in ONNX format, data in IDX format, and any necessary instructions.
1.5 Further Reading
If you are interested to know more about the theoretical underpinnings of Vehicle design, we recommend the following papers:
(Daggitt et al. 2024) Daggitt, M., Kokke. W., Atkey, R., Slusarz, N., Arnaboldi, L., Komendantskaya, E.: Vehicle: Bridging the Embedding Gap in the Verification of Neuro-Symbolic Programs. ARXIV, 2024.
(Casadio et al. 2022) Casadio, M., Komendantskaya, E., Daggitt, M.L., Kokke, W., Katz, G., Amir, G., Refaeli, I.: Neural network robustness as a verification property: A principled case study. In: Shoham, S., Vizel, Y. (eds.) Computer Aided Verification - 34th International Conference, CAV 2022, Haifa, Israel, August 7-10, 2022, Proceedings, Part I. Lecture Notes in Computer Science, vol. 13371, pp. 219–231. Springer (2022)
(Daggitt et al. 2023) Daggitt, M.L., Atkey, R., Kokke, W., Komendantskaya, E., Arnaboldi, L.: Compiling higher-order specifications to SMT solvers: How to deal with rejection constructively. In: Krebbers, R., Traytel, D., Pientka, B., Zdancewic, S. (eds.) Proceedings of the 12th ACM SIGPLAN International Conference on Certified Programs and Proofs, CPP 2023, Boston, MA, USA, January 16-17, 2023. pp. 102–120. ACM (2023).
(Slusarz et al. 2023) Natalia Slusarz, Ekaterina Komendantskaya, Matthew L. Daggitt, Robert J. Stewart, Kathrin Stark: Logic of Differentiable Logics: Towards a Uniform Semantics of DL. LPAR 2023. Proceedings of 24th International Conference on Logic for Programming, Artificial Intelligence and Reasoning, Manizales, Colombia, 4-9th June 2023, EPiC Series in Computing, vol. 94, pp. 473–493.
2 Getting Started with the Vehicle Specification Language
In this chapter we will introduce the basic features of the Vehicle specification language via the famous ACAS Xu verification challenge, first introduced in 2017 by Guy Katz et al. in “Reluplex: An Efficient SMT Solver for Verifying – Deep Neural Networks” (https://arxiv.org/pdf/1702.01135.pdf).
2.1 ACAS Xu
ACAS Xu stands for Airborne Collision Avoidance System for unmanned aircraft. The objective of the system is to analyse the aircraft’s position and distance relative to other aircraft and give collision avoidance instructions.
In particular, the following measurements are of importance:
- \rho: feet measuring the distance to intruder,
- \theta, \psi: radians measuring angle of intrusion,
- v_{own}, v_{vint}: feet per second - the speed of both aircrafts,
- \tau: seconds - time until loss of vertical separation,
- a_{prev}: previous advisory
as the following picture illustrates: 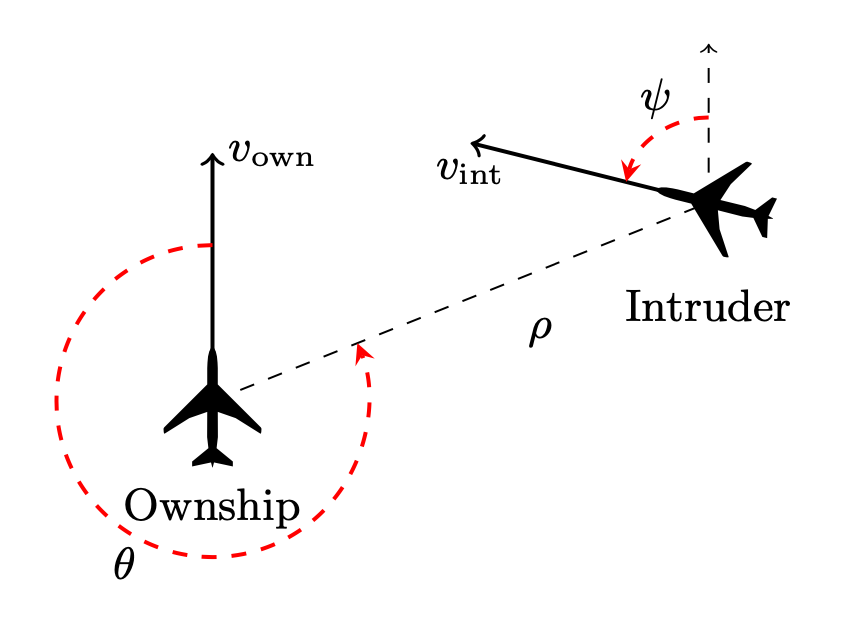
\theta and \psi are measured counter clockwise, and are always in the range [-\pi, \pi].
Based on these inputs, the system should produce one of the following instructions:
- clear-of-conflict (CoC),
- weak left,
- weak right,
- strong left,
- strong right.
In practice, the domains of \tau and a_{prev} are used to partition the input space into 45 discrete subspaces. Next a different neural network is trained to analyse the relation of input and output variables within each subspace, using previous historic data. Therefore each individual neural network uses only the first five input variables, and outputs a score for each of the output instructions. The instruction with the lowest score is then chosen.
Therefore each of the 45 ACASXu neural networks have the mathematical type N_{AX} : R^5 \rightarrow R^5. The exact architecture of the neural networks and their training modes are not important for this example, and so we will omit the details for now.
The original paper by Guy Katz lists ten properties, but for the sake of the illustration we will just consider the third property: If the intruder is directly ahead and is moving towards the ownship, the score for COC will not be minimal.
2.2 Basic Building Blocks in Vehicle
2.2.1 Types
Unlike many Neural Network verifier input formats, Vehicle is a typed language, and it is common for each specification file starts with declaring the types. In the ACAS Xu case, these are the types of vectors of rational numbers that the network will be taking as inputs and giving as outputs
type InputVector = Vector Rat 5
type OutputVector = Vector Rat 5
The Vector type represents a mathematical vector, or in
programming terms can be thought of as a fixed-length array. One
potentially unusual aspect in Vehicle is that the size of the
vector (i.e the number of items it contains) must be known statically at
compile time. This allows Vehicle to check for the presence of
out-of-bounds errors at compile time rather than run time.
The most general Vector type is therefore written as
Vector A n, which represents the type of vectors containing
n elements of type A. For example, in this
case Vector Rat 5 is a vector of length 5 that contains rational numbers.
Vehicle in fact has a comprehensive support for programming with vectors, which we will see throughout this tutorial. But the interested reader may go ahead and check the documentation pages for vectors: https://vehicle-lang.readthedocs.io/en/stable/language/vectors.html.
2.2.2 Networks
Given this, we can declare the network itself:
@network
acasXu : InputVector -> OutputVector
Networks are declared by adding a @network annotation to
a function declaration, as shown above. Note that no implementation for
the network is provided directly in the specification, and instead will
be provided later at compile time. However, the name acasXu
can still be used in the specification as any other declared function
would be. This follows the Vehicle philosophy that
specifications should be independent of any particular network, and
should be able to be used to train/test/verify a range of candidate
networks implementations.
2.2.3 Values
New values can be declared in Vehicle using the following syntax, where the first line provides the declaration’s type and the bottom line provides its definition.
<name> : <type>
<name> = <expr>
For example, as we’ll be working with radians, it is useful to define
a rational value called pi.
pi : Rat
pi = 3.141592
While in many cases, the types provide useful information to the reader, in general types can be omitted. For example, in this case it is cleaner to simply write the declaration as:
pi = 3.141592
The Vehicle compiler will then automatically infer the
correct Rat type.
2.2.4 Problem Space versus Input Space
Neural networks nearly always assume some amount of pre-processing of the input and post-processing of the output. In our ACASXu example, the neural networks are trained to accept inputs in the range [0, 1] and outputs are likewise in the range [0,1], i.e. the network does not work directly with units like m/s or radians, nor the 5 output instructions used in the description of the problem above. However, the specifications we write will be much more understandable if we can refer to values in the original units.
When we encounter such problems, we will say we encountered an instance of problem space / input space mismatch, also known as the embedding gap. If we were to reason on input vectors directly, we would be writing specifications in terms of the input space (i.e. referring to the neural network inputs directly). However, when reasoning about properties of neural networks, it is much more convenient to refer to the original problem. In this case specifications will be written in terms of the problem space. Being able to write specifications in the problem space (alongside the input space) is a feature that distinguishes Vehicle from majority of the mainstream neural network verifiers, such as e.g. Marabou, ERAN, or \alpha\beta-Crown. Let us see how this happens in practice.
We start with introducing the full block of code that will normalise input vectors into the range [0,1], and will explain significant features of Vehicle syntax featured in the code block afterwards.
For clarity, we define a new type synonym for unnormalised input vectors in the problem space.
type UnnormalisedInputVector = Vector Rat 5
Next we define the minimum and maximum values that each input can take. These correspond to the range of the inputs that the network is designed to work over. Note that these values are in the problem space.
minimumInputValues : UnnormalisedInputVector
minimumInputValues = [0, pi, pi, 100, 0]
maximumInputValues : UnnormalisedInputVector
maximumInputValues = [60261, pi, pi, 1200, 1200]
The above is the first instance of vector definition we encounter.
The type-checker will ensure that all vectors written in this way are of
the correct size (in this case, 5).
Then we define the mean values that will be used to scale the inputs:
meanScalingValues : UnnormalisedInputVector
meanScalingValues = [19791.091, 0.0, 0.0, 650.0, 600.0]
An alternative method for defining new vectors is to use the
foreach constructor, which is used to provide a value for
each index i. This method is useful if the vector has some
regular structure. For example, we can now define the normalisation
function that takes an unnormalised input vector and returns the
normalised version.
normalise : UnnormalisedInputVector -> InputVector
normalise x = foreach i .
(x ! i - meanScalingValues ! i) / (maximumInputValues ! i - minimumInputValues ! i)
Using this we can define a new function that first normalises the input vector and then applies the neural network:
normAcasXu : UnnormalisedInputVector -> OutputVector
normAcasXu x = acasXu (normalise x)
2.2.5 Functions
In the above block, we saw function definitions for the first time, so let us highlight the important features of the Vehicle language concerning functions.
2.2.5.1 Function declarations
Declarations may be used to define new functions. A declaration is of the form
<name> : <type>
<name> [<args>] = <expr>
Observe how all functions above fit within this declaration scheme.
2.2.5.2 Function types
Functions make up the backbone of the Vehicle language. The
function type is written A -> B where A is
the input type and B is the output type. For example, the
function validInput above takes values of the (defined)
type of UnnormalisedInputVector and returns values of type
Bool. The function normalise has the same
input type, but its output type is InputVector, which was
defined as a vector of rational numbers of size 5.
As is standard in functional languages, the function arrow associates
to the right so A -> B -> C is therefore equivalent
to A -> (B -> C).
2.2.5.3 Function application and composition
As in most functional languages, function application is written by
juxtaposition of the function with its arguments. For example, given a
function f of type Rat -> Bool -> Rat
and arguments x of type Rat and y
of type Bool, the application of f to
x and y is written f x y and this
expression has type Rat. This is unlike imperative
languages such as Python, C or Java where you would write
f(x,y).
Functions of suitable types can be composed. For example, given a
function acasXu of type
InputVector -> OutputVector, a function
normalise of type
UnnormalisedInputVector -> InputVector and an argument
x of type UnnormalisedInputVector the
application of acasXu to the InputVector
resulting from applying normalise x is written as
acasXu (normalise x), and this expression has type
OutputVector.
2.2.5.4 Pre-defined functions and predicates
Some functions are pre-defined in Vehicle. For example, the
above block uses multiplication *, division /
and vector lookup !. We have also seen the use of a
pre-defined “less than or equal to” predicate <= in the
definition of the function validInput (note its
Bool type).
2.2.6 Quantifying over indices
In the normalise declaration we saw the
foreach construct which constructs a vector given the
definition of the element at each index i. We can use the
similar forall to quantify over all indices and return a
Bool which is true if the predicate holds for
all indices and false otherwise. For example, having
defined the range of minimum and maximum values, we can define a simple
predicate saying whether a given input vector is in the right range:
validInput : UnnormalisedInputVector -> Bool
validInput x = forall i . minimumInputValues ! i <= x ! i <= maximumInputValues ! i
Equally usefully, we can write a function that takes an output index
i and an input x and returns true if output
i has the minimal score, i.e., neural network outputs
instruction i.
minimalScore : Index 5 -> UnnormalisedInputVector -> Bool
minimalScore i x = forall j . i != j => normAcasXu x ! i < normAcasXu x ! j
Here the Index 5 refers to the type of indices into
Vectors of length 5, and implication => is
used to denote logical implication. Therefore this property says that
for every other output index j apart from output index
i we want the score of action i to be strictly
smaller than the score of action j.
2.2.7 Naming indices
As ACASXu properties refer to certain elements of input and output vectors, let us give those vector indices some suggestive names. This will help us to write a more readable code:
distanceToIntruder = 0 -- measured in metres
angleToIntruder = 1 -- measured in radians
intruderHeading = 2 -- measured in radians
speed = 3 -- measured in metres/second
intruderSpeed = 4 -- measured in meters/second
The fact that all vector types come annotated with their size means
that it is impossible to mess up indexing into vectors, e.g. if you
changed distanceToIntruder = 0 to
distanceToIntruder = 5 the specification would fail to
type-check as 5 is not a valid index into a
Vector of length 5.
Similarly, we define meaningful names for the indices into output vectors.
clearOfConflict = 0
weakLeft = 1
weakRight = 2
strongLeft = 3
strongRight = 4
2.3 Property Definition in Vehicle
We now make up for the time invested into learning the Vehicle syntax, as stating a verification property becomes very easy. Let us now look at the property again:
If the intruder is directly ahead and is moving towards the ownship, the score for COC will not be minimal.
We first need to define what it means to be directly ahead and moving towards. The exact ACASXu definition can be written in Vehicle as:
directlyAhead : UnnormalisedInputVector -> Bool
directlyAhead x =
1500 <= x ! distanceToIntruder <= 1800 and
-0.06 <= x ! angleToIntruder <= 0.06
movingTowards : UnnormalisedInputVector -> Bool
movingTowards x =
x ! intruderHeading >= 3.10 and
x ! speed >= 980 and
x ! intruderSpeed >= 960
Note the reasoning in terms of the “problem space”, i.e. the use of unnormalised input vectors.
We have already encountered the vector lookup ! before;
but now we have a new predefined comparison function,
>=, “greater than or equal to”. The connective
and is a usual Boolean connective (note the type of the
function is Bool).
There is little left to do, and we finish our mini-formalisation with the property statement:
@property
property3 : Bool
property3 = forall x .
validInput x and directlyAhead x and movingTowards x =>
not (minimalScore clearOfConflict x)
To flag that this is the property we want to verify, we use the label
@property, we have seen this notation before when we used
@network to annotate the neural network declaration. The
final new bit of syntax we have not yet discussed is the quantifier
forall.
2.3.1 Infinite quantifiers
One of the main advantages of Vehicle is that it can be used
to state and prove specifications that describe the network’s behaviour
over an infinite set of values. We have already seen the
forall operator used in the declaration
validInput – however, there it was quantifying over a
finite number of indices.
The forall in the property above is a very different
beast as it is quantifying over an “infinite” number of
Vector Rat 5s. The definition of property3
brings a new variable x of type Vector Rat 5
into scope. The variable x has no assigned value and
therefore represents an arbitrary input of that type.
Vehicle also has a matching quantifer
exists.
2.4 How to run Vehicle
To verify this property, we only need to have:
- a verifier installed (at the moment of writing Vehicle has integration with Marabou);
- the actual network or networks that we wish to verify. These need to be supplied in an ONNX format, one of the standard formats for representing trained neural networks.
Having these suitably installed or located, it only takes one command
line to obtain the result (note the vcl file, where we have
written the above specification):
vehicle \
verify \
--specification acasXu.vcl \
--verifier Marabou \
--network acasXu:acasXu_1_7.onnx \
--property property3
Vehicle passes the network, as well as a translation of our
specification, to Marabou, and we obtain the result –
property3 does not hold for the given neural network,
acasXu_1_7.onnx:
Verifying properties:
property3 [======================================================] 1/1 queries
result: ✗ - counterexample found
x: [1799.9886669999978, 5.6950779776e-2, 3.09999732192, 980.0, 960.0]
Furthermore, Vehicle gives us a counter-example in the
problem space! In particular an assignment for the quantified variable
x that falsifies the assignment.
2.5 Exercises
We will use symbols (*), (**) and (***) to rate exercise difficulty: easy, moderate and hard.
The exercises assume that you already installed Vehicle as described in vehicle documentation.
2.5.1 Exercise (*)
Start by simply running the code that was discussed in the above
chapter. It is available from the examples section of the
tutorial
repository
Repeat the steps described in this chapter: download the Vehicle specification and the network, and verify the ACAS Xu Property 3.
Did it work? If yes, you are ready to experiment with your own specifications.
2.5.2 Exercise (**). Problem Space versus Input/Output Space
We discussed an instance of the embedding gap when verifying Property 3. In particular, we reasoned in terms of the problem space, but verified the network trained on the input space.
Property 1 in the Acas Xu library is an example where the problem space and the output space deviate, as well. This makes Property 1 specification somewhat harder.
For your first exercise, define Property 1 in Vehicle, paying attention to careful handling of the embedding gap.
ACAS Xu Propery 1: If the intruder is distant and is significantly slower than the ownship, the score of a COC advisory will always be below a certain fixed threshold.
Taking the original thresholds, this boils down to:
(\rho \geq 55947.691) \wedge (v_{own} \geq 1145) \wedge (v_{int} \leq 60) \Rightarrow \text{the score for COC is at most} 1500
Note: The ACAS Xu neural network outputs are scaled as follows: given an element x of the output vector, we scale it as: \frac{x - 7.518884}{373.94992}.
To run the verification queries, please use the networks available from the tutorial repository.
2.5.3 Exercise (**). The full ACAS Xu chellenge in one file
Why not trying to state all 10 ACAS
Xu properties in one .vcl file? Try running the
verification query in Vehicle using all 10 properties. You can find them all here:
“Reluplex: An Efficient SMT Solver for Verifying – Deep Neural
Networks” (https://arxiv.org/pdf/1702.01135.pdf)
2.5.4 Exercise (***). Your first independent Vehicle specification
- On the tutorial
repository, find the ONNX model,
iris_model.onnxtrained on the famous Iris data set: https://en.wikipedia.org/wiki/Iris_flower_data_set. Find also the data set in theidxformat (cf. tutorial repository). - Using the Wikipedia page or other sources, examine the data set, and try to define a few “obvious properties” that should hold for a model that does its classification.
- Write those properties as a Vehicle specification, ensure it type checks. See the Vehicle Manual for how to run type checking.
- Using the Vehicle command line, verify your specification, i.e. check whether the properties hold.
3 Proving Neural Network Robustness
3.1 Neural Network Robustness as a Verification Property
In this chapter we will learn about the problem that has received significant attention within the machine learning community: the problem of robustness of neural networks to out-of-distribution shifts, also known as “robustness to adversarial attacks”. The problem was famously raised by Christian Szegedy and his co-authors in 2013 in the paper “Intriguing properties of neural networks”
So, here is the problem. Suppose we are given a data set \mathcal{X} for classification of images, it consists of pairs (\mathbf{x}, \mathbf{y}), where \mathbf{x} \in \mathbb{R}^n is an input, and \mathbf{y} \in \mathbb{R}^m is the desired output. It is assumed that the outputs \mathbf{y} are generated from \mathbf{x} by some function \mathcal{H} : \mathbb{R}^n → \mathbb{R}^m and that \mathbf{x} is drawn from some probability distribution over \mathbb{R}^n.
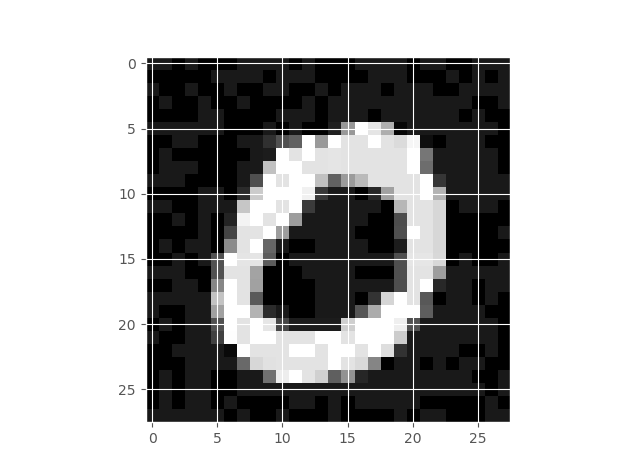
Let us take as an example the famous MNIST data set by LeCun et al. The images look like this:

As we have already discussed in the previous chapter, a neural network is a function f : \mathbb{R}^n → \mathbb{R}^m parametrised by a set of weights \mathbf{w}. The goal of training is to use the dataset \mathcal{X} to find weights \mathbf{w} such that f approximates \mathcal{H} well over input regions with high probability density.
When we train a neural network to be highly accurate on both the training and the test sets, we emprically test:
- how well the neural network can in principle approximate \mathcal{H} (we do this by measuring its accuracy on the training set);
- how well that learnt hypothesis generalises to yet unseen data (we do this by measuring the accuracy on the test set).
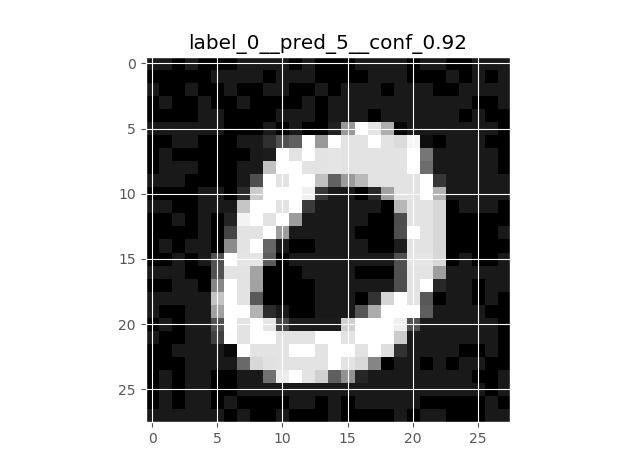
Coming to our example, if my neural network has a 99 % accuracy on the MNIST data set, I should be satisfied that it learnt what a hand-written digit is. Szegedy et al were the first to show systematically that this is not the case: take the image on the left (below), which is classified with high confidence as “0”, apply perturbation on the middle to get the image on the right, and your neural network will give a 94 % confidence that it sees a “5” on the right, even despite the fact that the image did not change the class (for the human eye):
| Original MNIST Image | Perturbation | Resulting Perturbed Image |
|---|---|---|
 |
 |
 |
This experiment can be replicated for any data set and any neural network, no matter how accurate it is.
The root of the problem is: the image on the right no longer belongs to the probability distribution that the network has learnt (whether or not the image looks the same to a human observer). We could phrase it differently: an ideal probability distribiution \mathcal{H} that is “learnt” by a “human” accounts not only for the images we obtained as part of the dataset \mathcal{X}, but also involves an implicit assumption that “semantically” similar images belong to the same class.
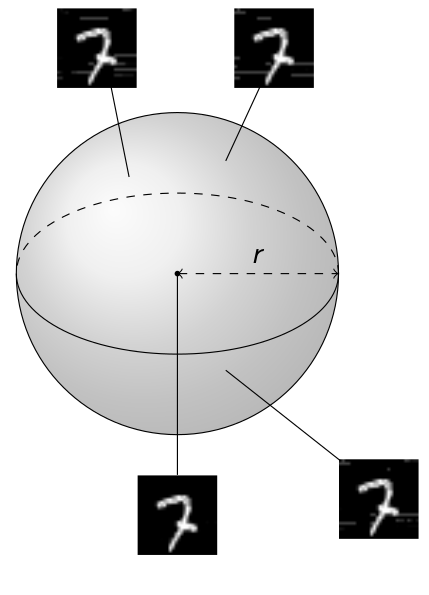
The simplest way to capture this implicit assumption is to formulate a verification property that insists that all similar images (images within an \epsilon distance of each other in \mathbb{R}^n) are classified similarly. This property is often called \epsilon-ball robusness. For every image in the dataset, we assume we can “draw” a small \epsilon-ball around it, and guarantee that within that \epsilon-ball classification of the network does not change much (the ball’s radius below is given by the chosen \epsilon):
| \epsilon-ball around a number “7” in MNIST |
|---|
 |
Formally, we define an \epsilon-ball around an image \hat{\mathbf{x}} as:
\mathbb{B}(\hat{\mathbf{x}}, \epsilon) = [ \mathbf{x} \in \mathbb{R}^n: |\hat{\mathbf{x}}-\mathbf{x}| \leq \epsilon ]
where | ... | is a distance function (or L-norm) in \mathbb{R}^n, such as Euclidean distance or L_{\infty}-norm.
It now remains to define the property “classification of f does not change much”. The paper by Casadio et al. summarises a few options for this definition. The simplest is the Classification Robustness that requires that all images within any given \epsilon-ball are classified as the same class. We will consider this property in detail, and will take a few other properties from Casadio et al. as an exercise.
3.2 Formalising \epsilon-ball robustness for MNIST networks in Vehicle
We note that \epsilon-ball robustness as a verification property bears some similarity to the ACAS Xu example that we have already covered in Chapter 1. In particular, both verification properties impose constraints on the output regions of the neural networks, assuming some constraint on their input regions. (Both problems are therefore amenable to a range of interval propagation and abstract interpretation methods, see this survey for further details.) From the point of view of the property specification, which is our main concern here, there are three main differences between these two examples:
ACAS Xu did not have to refer to a dataset \mathcal{X}; \epsilon-ball robustness, however, is formulated relative to the images given in the data set. We will see how Vehicle can be used to handle properties that refer directly to the data sets.
MNIST, as many other data sets used in Computer Vision, has images represented as 2D arrays. Such data sets often require Convolutional Neural Networks (CNNs) that are best designed to deal with 2D and 3D data. In terms of property specification, we will see Vehicle’s support for 2D arrays, which comes for free with its general type infrastructure.
Finally, the MNIST specification involves two parameters that we may want to pass or infer at the compilation time rather than hard-code within the spec. These are the \epsilon and the number of data points (\epsilon-balls) we wish to check (the number is at most the size of the entire data set). We will see how such parameters are defined and used in Vehicle.
3.2.1 2D Arrays in Vehicle
Starting a specification for MNIST data set follows the same pattern as we have seen in Chapter 1, only this time we declare inputs as 2D arrays:
type Image = Tensor Rat [28, 28]
type Label = Index 10
As before, we define valid inputs, this time making a mild adaptation to 2D arrays and assuming all pixel values are normalised between 0 and 1:
validImage : Image -> Bool
validImage x = forall i j . 0 <= x ! i ! j <= 1
The output of the network is a score for each of the digits 0 to 9.
@network
classifier : Image -> Vector Rat 10
We note again the use of the syntax for @network,
marking the place where Vehicle interacts with an external tool
(this time most likely with Python Tensorflow).
The classifier advises that input image x has label
i if the score for label i is greater than the
score of any other label j:
advises : Image -> Label -> Bool
advises x i = forall j . j != i => classifier x ! i > classifier x ! j
This completes the basic description if the data set and the model architecture in Vehicle. We are ready to define verification properties.
3.2.2 Definition of Robustness Around a Point
First we define the parameter epsilon that will
represent the radius of the balls that we verify. Note that we declare
this as a parameter which allows the value of epsilon to be
specified at compile time rather than be fixed in the specification. We
again use the syntax @ to communicate this information
externally:
@parameter
epsilon : Rat
Next we define what it means for an image x to be in a
ball of size epsilon. The definition below uses the L_{\infty} norm, defined as:
|\mathbf{x}|_{\infty} = max (\mathbf{x})
where max (\mathbf{x}) computes the maximum element of \mathbf{x}. Below, we shortcut a bit the calculation of |\mathbf{x}|_{\infty} being bounded by \epsilon and simply require that all vector elements are bounded by \epsilon:
boundedByEpsilon : Image -> Bool
boundedByEpsilon x = forall i j . -epsilon <= x ! i ! j <= epsilon
Using the Eucledian distance would require a slightly more complicated definition, which we will do as an exercise.
We now define what it means for the network to be robust around an
image x that should be classified as y.
Namely, we define that for any perturbation no greater than \epsilon, if the perturbed image is still a
valid image then the network should still advise label y
for the perturbed version of x.
robustAround : Image -> Label -> Bool
robustAround image label = forall pertubation .
let perturbedImage = image - pertubation in
boundedByEpsilon pertubation and validImage perturbedImage =>
advises perturbedImage label
Again, note the use of a quantifier forall that ranges
over an infinite domain of images of type Image.
3.3 Definition of Robustness with Respect to a Dataset
We first specify parameter n , which stands for the size
of the training dataset. Unlike the earlier parameter
epsilon, we set the infer option of the
parameter n to ‘True’. This means that it does not need to
be provided manually but instead will be automatically inferred by the
compiler. In this case it will be inferred from the training
datasets.
@parameter(infer=True)
n : Nat
We next declare two datasets, the training images and the
corresponding training labels. Note that we use the previously declared
parameter n to enforce that they are of the same size:
@dataset
trainingImages : Vector Image n
@dataset
trainingLabels : Vector Label n
Again we note the use of syntax that involves @ flagging
Vehicle’s connection with an external tool or object – in this
case, the data set is defined externally.
We then say that the network is robust for this data set if
it is robust around every pair of input images and output labels. Note
once again the use of the foreach keyword when quantifying
over the index i in the dataset. Whereas
forall would return a single Bool,
foreach constructs a Vector of booleans,
ensuring that Vehicle will report on the verification status of
each image in the dataset separately. If forall was
omitted, Vehicle would only report if the network was robust
around every image in the dataset, a state of affairs which is
unlikely to be true.
@property
robust : Vector Bool n
robust = foreach i . robustAround (trainingImages ! i) (trainingLabels ! i)
3.4 Running the Verification Query
In order to run Vehicle, we need to provide:
- the specification file,
- the network in ONNX format,
- the data in idx format,
- and the desired \epsilon value.
The tutorial files contain two Python scripts that show how to
convert Tensorflow Neural Networks into ONNX format; and images
– into .idx files. These are the formats expected by
Vehicle. You can use the ones we provide, or generate your own.
Having obtained these, the following command line will take care of
verification of the network mnist-classifier.onnx, for data
sets images.idx and labels.idx and \epsilon = 0.005:
vehicle verify \
--specification examples/mnist-robustness/mnist-robustness.vcl \
--network classifier:examples/mnist-robustness/mnist-classifier.onnx \
--parameter epsilon:0.005 \
--dataset trainingImages:examples/mnist-robustness/images.idx \
--dataset trainingLabels:examples/mnist-robustness/labels.idx \
--verifier Marabou
For the first two images in your data set, the output will look as follows:
Verifying properties:
robust [================================================] 9/9 queries complete
robust [================================================] 9/9 queries complete
Result: true
robust: 2/2 verified
✓ robust!0
✓ robust!1
The reader may have guessed at this pont that, as we make \epsilon larger, fewer and fewer examples will staisfy the property. Chapter 3 will look into methods that can be used to train networks to satisfy robustness for larger \epsilon.
3.5 Exercises
3.5.1 Exercise (*): Run the Chapter code
As usual, your first task is to repeat the steps described in this
chapter: download the Vehicle specification, the network, the
data, and verify robustness of the given network on given data. All code
is available from the examples section of the tutorial
repository
3.5.2 Exercise (*) : Experimenting with \epsilon-balls of different size
Try experimenting with different values of \epsilon, for example, try \epsilon = 0.005, 0.01, 0.05, 0.1, 0.5. Make conclusions.
3.5.3 Exercise (**) : Getting a statistical evaluation of robustness with respect to the given data set, for various \epsilons
(This exercise is technically very simple, but the required number of experiments may take a few hours to run. We recommend you run it at home rather than during the live exercise sessions).
The previous exercise could be transformed into a proper empirical
evaluation of robustness of the model for the data set. To do this,
include more than 2 images into your idx file. A script for
generating idx files is available in
the supporting materials.
Assuming you created an idx file with, for example, 500
images, run Vehicle on this file, and collect statistics for
\epsilon = 0.005, 0.01, 0.05, 0.1, 0.5.
You should be able to populate a table that looks like this:
| \epsilon = 0.005 | \epsilon = 0.01 | \epsilon = 0.05 | \epsilon = 0.1 | \epsilon = 0.5 | |
|---|---|---|---|---|---|
| Success rate: | 100.0 % (500/500) | ?? % (???/500) | ?? % (???/500) | ? % (??/500) | 0 % (0/500) |
This is your first proper empirical evaluation of the given neural network for the given data set! This kind of evaluation is reported in international competitoions such as VNNComp and in research papers.
Make conclusion about feasibility and success rates of \epsilon-ball robustness, and the speed with which verification success deteriorates with the growing \epsilon.
3.5.4 Exercise (*) : Strong Classification Robustness in Vehicle
Using the same .vcl file as in all previous exercises,
define and verify in Vehicle the propety of Strong
Classification Robustness, that requires, for all \mathbf{x} in the \epsilon-ball of \hat{\mathbf{x}}, that f(\mathbf{x})_i \leq \eta, for some small
\eta. We now assemble the
desired_strong classification robustness_ property definition:
Given an \hat{\mathbf{x}} \in \mathcal{X},
\forall \mathbf{x}. |\hat{\mathbf{x}}-\mathbf{x}| \leq \epsilon \Longrightarrow f(\mathbf{x})_i \leq \eta
We refer the interested reader for a more detailed discussion of different robustness properties in:
Marco Casadio, Ekaterina Komendantskaya, Matthew L. Daggitt, Wen Kokke, Guy Katz, Guy Amir, Idan Refaeli: Neural Network Robustness as a Verification Property: A Principled Case Study. CAV (1) 2022: 219-231.
Xiaowei Huang, Daniel Kroening, Wenjie Ruan, James Sharp, Youcheng Sun, Emese Thamo, Min Wu, Xinping Yi. A Survey of Safety and Trustworthiness of Deep Neural Networks: Verification, Testing, Adversarial Attack and Defence, and Interpretability. J. of Computer Science Review, 2018.
3.5.5 Exercise (**): Explore Other Definitions of Robustness
Use Vehicle to define other forms of Robustness property from Casadio et al.
Please note: although the Vehicle language is rich enough to compile all the robustness definitions, not all definitions will be feasible for Marabou that can have only one occurence of a neural network per specification.
3.5.6 Exercise (**): Other Distances in Vehicle
Re-define the classification and standard robustness properties by using some different notion of distance, e.g. the Euclidean distance, instead of the L_{\infty} norm.
Please note: although the Vehicle language is rich and allows such extensions, not all specifications will be feasible for Marabou that works with linear real arithmetic.
3.5.7 Exercise (*) Practicing to write property specifications
To test your understanding of the robustness property, try completing the robustness verification in this file.
3.5.8 Exercise (***): Conduct a complete “training - verification” experiment from start to finish
This exercise can be hard or simple, depending how much help you get from the model solution provided as sources!
We will work with the Fashion MNIST data set.
Either:
- download the data set, train a model from scratch, generate
onnxandidxfiles; or - obtain the model and
idxfiles directly from the directory with the supporting materials
Once this is done, define the spec and verify its robustness. Experiment with different values of \epsilon and different definitions of robustness.
4 Property-Driven Training
4.1 Motivation
We finished the last chapter with a conjecture concerning diminishing robustness verification success with increasing values of \epsilon. Let us now see, using a concrete example, how soon the success rate declines.
The last exercise of the previous chapter gave us a property specification for robustness of ``Fashion MNIST” models. We propose now to look into the statistics of verifying one of such models on 500 examples from the data set. To obtain quicker verification times, let us use a Fashion MNIST model with one input layer of 32 neurons, and one output layer of 10 neurons (the tutorial files contain the model if you wish to check it). Running Vehicle, we obtain the following success rates:
| \epsilon = 0.01 | \epsilon = 0.05 | \epsilon = 0.1 | \epsilon = 0.5 |
|---|---|---|---|
| 82.6 % (413/500) | 29.8 % (149/500) | 3.8 % (19/500) | 0 % (0/500) |
As we see in the table, verifiability of the property deteriorates quickly with growing \epsilon. Yet, for majority of practical applications, it is desirable to have a larger \epsilon, as this increases the chance that new yet unseen data points will fall within the verified subspaces of the input vector space.
Can we re-train the neural network to be more robust within a desirable \epsilon? The long tradition of robustifying neural networks in machine learning has a few methods ready, for example, to re-train the networks with new data set that was augmented with images within the desired \epsilon-balls, or to generate adversarial examples (sample images closest to the decision boundary) within the given \epsilon-balls during training.
Let us look closer into this.
4.2 Robustness Training
4.2.1 Data Augmentation
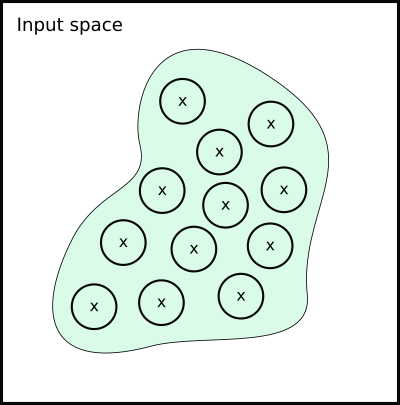
Suppose we are given a data set \mathcal{D} = \{(\mathbf{x}_1, y_1), \ldots , (\mathbf{x}_n, y_n)\}. Prior to training, we can generate new training data samples within \epsilon-balls of the existing data and label them with the same output as the original data. Then we can use our usual training methods with this new augmented data set ((Shorten and Khoshgoftaar 2019)).
However, this method maybe problematic for verification purposes. Let us have a look at its effect, pictorially. Suppose this is the manifold that corresponds to \mathcal{D} (crosses are the original data points, and circles are the \epsilon-balls around them):
Remember that we sampled our new data from these \epsilon-balls. But suppose your true decision boundary runs over the manifold like this:
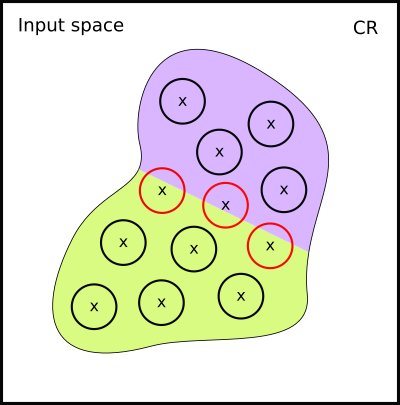
We have a problem, because some of the data points we sampled from the suddenly have wrong labels!
Actually, it maybe even worse. Depending how our data lies on the manifold, we may have even generated inconistent labelling. Here is the example when this happens:
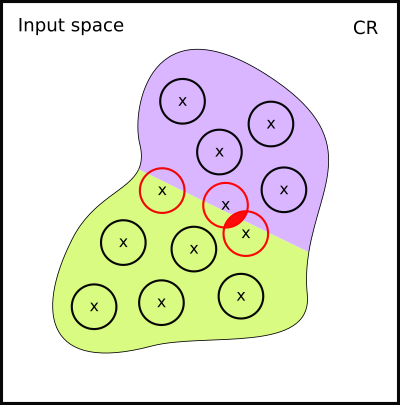
It seems data augmentation is not general enough for Vehicle, and only works correctly if strong assumptions about the underlying manifold are taken.
4.2.2 Adversarial Training
It would be nice to somehow reflect the fact of proximity to the decision boundary in our training! The closer the point is to the decision boundary, the less certain the neural network should be about its class:
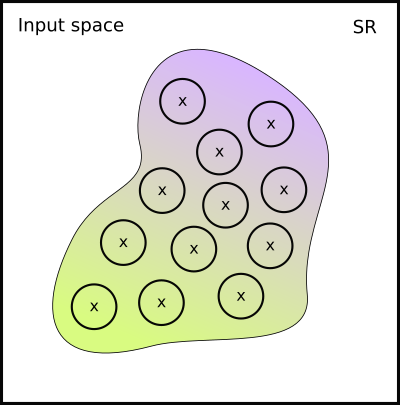
However, using data labels as a method is unfit for the task. We cannot achieve the effect we are looking for with data augmentation. We have to modify our training algorithm instead (Goodfellow, Shlens, and Szegedy 2015).
4.2.2.1 Loss Function
Given a data set \mathcal{D} and a
function
{f_{\theta}: \mathbb{R}^n \rightarrow
\mathbb{R}^m} (with optimisation parameters \theta), a loss function
\mathcal{L}: \mathbb{R}^n \times \mathbb{R}^m \rightarrow \mathbb{R}
computes a penalty proportional to the difference between the output of f_{\theta} on a training input \hat{\mathbf{x}} and a desired output \mathbf{y}.
The reader will find an excellent exposition of adversarial training in this tutorial: (Kolter and Madry 2018).
4.2.2.2 Example: Cross-Entropy Loss
Given a function {f_{\theta}: \mathbb{R}^n \rightarrow [0,1]^m}, the cross-entropy loss is defined as
\mathcal{L}_{ce}(\hat{\mathbf{x}}, \mathbf{y}) = - \Sigma_{i=1}^{m} \mathbf{y}_i \; log(f_{\theta}(\hat{\mathbf{x}})_i)
where \mathbf{y}_i is the true probability for class i and f_{\theta}(\hat{\mathbf{x}})_i is the probability for class i as predicted by f_{\theta} when applied to \hat{\mathbf{x}}.
4.2.2.3 Adversarial Training for Robustness
Gradient descent minimises loss \mathcal{L}(\hat{\mathbf{x}}, \mathbf{y}) between the predicted value f_{\theta}(\hat{\mathbf{x}}) and the true value \mathbf{y}, for each entry (\hat{\mathbf{x}}, \mathbf{y}) in \mathcal{D}. It thus solves the optimisation problem:
\min_{\theta} \mathcal{L}(\hat{\mathbf{x}}, \mathbf{y})
For adversarial training, we instead minimise the loss with respect to the worst-case perturbation of each sample in \mathcal{D}. We replace the standard training objective with:
\min_{\theta} [ \max_{\mathbf{x} : |\mathbf{x} - \hat{\mathbf{x}}| \leq \epsilon} \mathcal{L}(\mathbf{x}, \mathbf{y})]
The inner maximisation is done by projected gradient descent (PGD), that ``projects” the gradient of \mathcal{L} on \hat{\mathbf{x}} in order to perturb it and get the worst \mathbf{x}.
4.2.3 Adversarial Training and Verification
Adversarial training is almost the right solution! Its main limitation turns out to be the logical property it optimises for. Recall that we may encode an arbitrary property in Vehicle. However, as we discovered in (Casadio et al. 2022), the projected gradient descent can only optimise for one concrete property. Recall the property of \epsilon-ball robustness was defined as: \forall \mathbf{x} \in \mathbb{B}(\hat{\mathbf{x}}, \epsilon). robust(f(\mathbf{x})). It turns out that adversarial training determines the definition of robust to be |f(\mathbf{x}) - f(\hat{\mathbf{x}})| \leq \delta.
Is there any way to generate neural network optimisers for any given logical property?
4.3 Logical Loss Functions
The main idea is that we would like to co-opt the same gradient-descent algorithm that is used to train the network to fit the data to also train the network to obey the specification.
4.3.1 Logical Loss Function: Simple Example
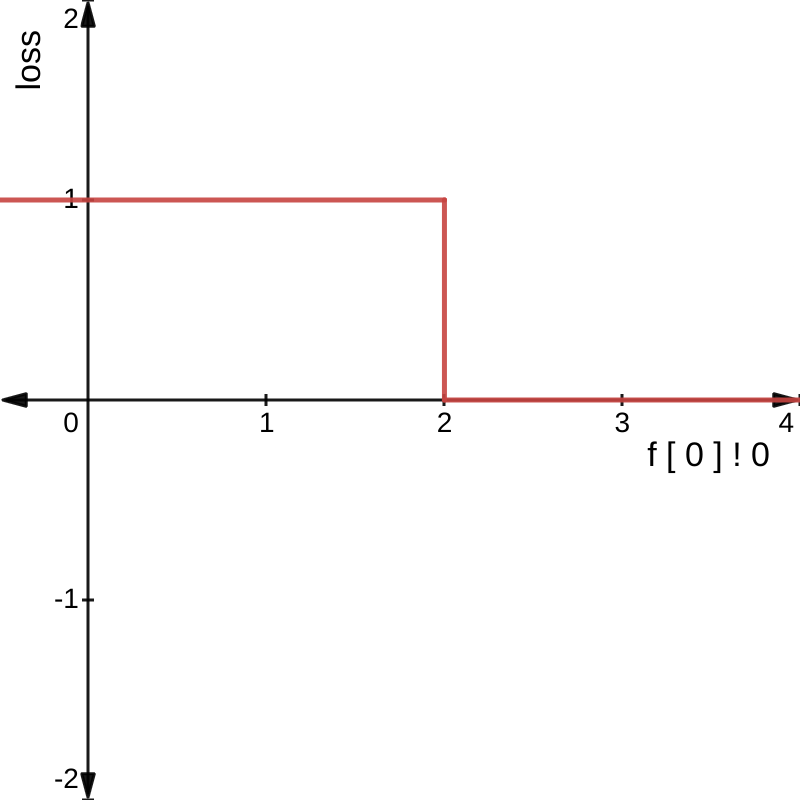
Consider the very simple example specification:
@network
f : Vector Rat 1 -> Vector Rat 1
@property
greaterThan2 : Bool
greaterThan2 = f [ 0 ] ! 0 > 2
This statement is either true or false, as shown in the left graph below:
However, what if instead, we converted all Bool values
to Rat, where a value greater than 0 indicated
false and a value less than 0 indicated true? We could then
rewrite the specification as:
greaterThan2 : Rat
greaterThan2 = f [ 0 ] ! 0 - 2
If we then replot the graph we get the following:
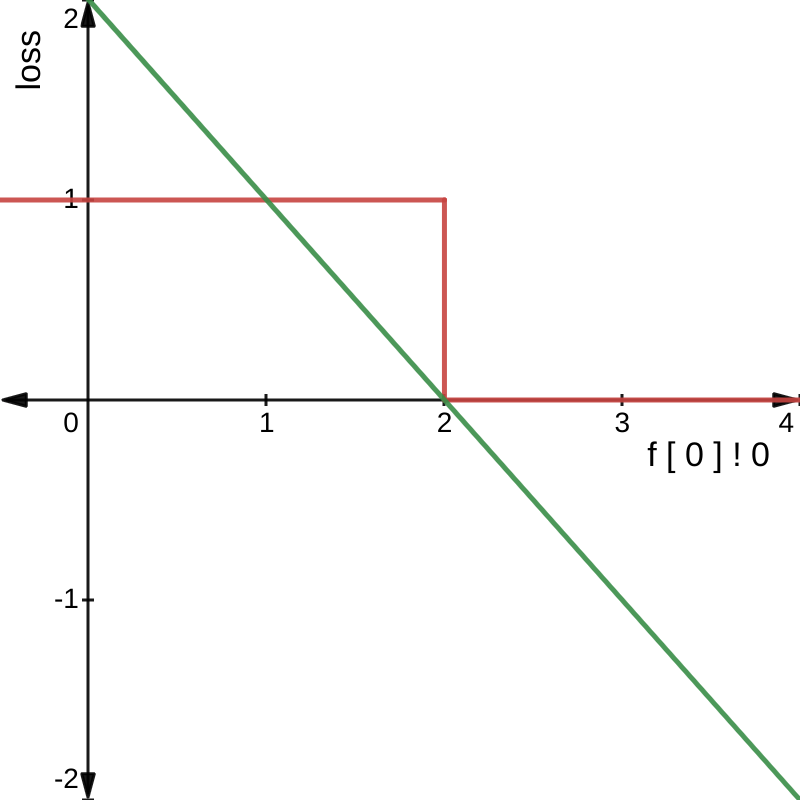
Now we have a useful gradient, as successfully minimising
f [ 0 ] ! 0 - 2 will result in the property
greaterThan2 becoming true.
This is the essence of logical loss functions: convert all booleans and operations over booleans into equivalent numeric operations that are differentiable and whose gradient’s point in the right direction.
4.3.2 Differentiable Logics
Traditionally, translations from a given logical syntax to a loss function are known as “differentiable logics”, or DLs. One of the first attempts to translate propositional logic specifications to loss functions was given in (Xu et al. 2018) and was generalised to a fragment of first-order logic in (Fischer et al. 2019). Later, this work was complemented by giving a fuzzy interpretation to DL by (Krieken, Acar, and Harmelen 2022) and (Slusarz et al. 2023) proposed generalisation for the syntax and semantics of DL, with a view of encoding all previously presented DLs in one formal system, and comparing their theoretical properties.
Vehicle has several different differentiable logics from the literature available, but will not go into detail about how they work here.
Instead, we explain the main idea by means of an example. Let us define a very simple differentiable logic on a toy language
p := p\ |a\ \leq\ a|\ p \land p\ |\ p \Rightarrow p
One possible DL (called Product DL in (Krieken, Acar, and Harmelen 2022)) for it can be defined as:
\mathcal{I}(a_1 \leq a_2) := 1-\max(\frac{a_1 -a_2}{a_1 + a_2}, 0)
\mathcal{I}(p_1 \land p_2) := \mathcal{I}(p_1) * \mathcal{I}(p_2)
\mathcal{I}(p_1 \Rightarrow p_2) := 1 - \mathcal{I}(p_1) + \mathcal{I}(p_1) * \mathcal{I}(p_2)
So, an example of this translation is:
\mathcal{I} (| f(\mathbf{x}) - f(\hat{\mathbf{x}})| \leq \delta) = 1 - \max (\dfrac{| f(\mathbf{x}) - f(\hat{\mathbf{x}})| - \delta}{| f(\mathbf{x}) - f(\hat{\mathbf{x}})| + \delta},0).
4.4 Logical Loss Functions in Vehicle
We now have all the necessary building blocks to define Vehicle approach to property-driven training. We use the formula:
Vehicle Training = Differentiable Logics + Projected Gradient Descent
In Vehicle, given a property \forall \mathbf{x}. \mathcal{P}(\mathbf{x}) \Rightarrow \mathcal{S}(\mathbf{x}), we replace the usual PGD training objective with
\min_{\theta} [ \max_{\mathbf{x} \in \mathbb{H}_{\mathcal{P}(\mathbf{x})}} \mathcal{L}_{\mathcal{S}(\mathbf{x})}(\mathbf{x}, \mathbf{y})] where
\mathbb{H}_{\mathcal{P}(\mathbf{x})} is a hyper-shape that corresponds to the pre-condition \mathcal{P}(\mathbf{x}) and
\mathcal{L}_{\mathcal{S}(\mathbf{x})} is obtained by DL-translation of the post-condition \mathcal{S}(\mathbf{x}).
Let us see how this works for the following definition of robustness: \forall \mathbf{x}. |\mathbf{x} - \hat{\mathbf{x}}| \leq \epsilon \Rightarrow |f(\mathbf{x}) - f(\hat{\mathbf{x}})| \leq \delta
The definition of the optimisation problem above instantiates by taking:
\mathbb{H}_{\mathcal{P}(\mathbf{x})} given by the \epsilon-cube around \hat{\mathbf{x}}
and, given any DL translation \mathcal{I}, the loss function \mathcal{L}_{\mathcal{S}(\mathbf{x})} = \mathcal{I} ( || f(\mathbf{x}) - f(\hat{\mathbf{x}})|| \leq \delta)
4.5 Coding Example: generating a logical loss functions for mnist-robustness in Vehicle
To generate a logical loss function usable in Python, we will use Vehicle’s Python bindings that come pre-installed.
We open a new Python file and write:
from vehicle_lang.compile import Target, to_python
spec = to_python(
"mnist-robustness.vcl",
target=Target.LOSS_DL2,
samplers={"pertubation": sampler_for_pertubation},
)
robust_loss_fn = spec["robust"]which generates the loss function representing the logical loss
function for the property robust.
This can then be used in a standard training loop:
model = tf.Sequential([tf.Input(shape=(28,28)), tf.Dense(units=28), tf.Output(units=10)])
for epoch in range(num_epochs):
for x_batch_train, y_batch_train in train_dataset:
with tf.GradientTape() as tape:
# Calculate standard cross entropy loss
outputs = model(x_batch_train, training=True)
ce_loss_value = ce_batch_loss(y_batch_train, outputs)
# Calculate the robustness loss
robust_loss_value = robust_loss_fn(
n=len(x_batch_train),
classifier=model,
epsilon=0.001,
trainingImages=x_batch_train,
trainingLabels=y_batch_train,
)
weighted_loss = 0.5 * ce_loss_value + 0.5 * robust_loss_value
grads = tape.gradient(weighted_loss, model.trainable_weights)
optimizer.apply_gradients(zip(grads, model.trainable_weights))5 Exporting to Agda
5.1 Motivation
In this chapter, we will look at how to export a Vehicle specification to Agda. Why is this useful? In the previous chapters we’ve been studying about how to verify neural networks in isolation. However, frequently neural networks are used as a part of a larger program whose correctness we would also like to verify. Vehicle is clearly not designed to reason about the correctness of arbitrary programs, and therefore we need to link to tools that are. Agda, a powerful interactive theorem prover, is one such tool and by exporting Vehicle specifications to Agda code we can construct safety proofs for software systems whose correctness depends on the correctness of a neural network.
5.2 An example
As an example we will use a modified version of the verification problem presented by Boyer, Green and Moore (Boyer, Green, and Moore 1990). In this scenario an autonomous vehicle is travelling along a straight road of width 6 parallel to the x-axis, with a varying cross-wind that blows perpendicular to the x-axis. The vehicle has an imperfect sensor that it can use to get a (possibly noisy) reading on its position on the y-axis, and can change its velocity on the y-axis in response. The car’s controller takes in both the current sensor reading and the previous sensor reading and its goal is to keep the car on the road.
Given this, the aim is to prove the following theorem:
Theorem 1: assuming that the wind-speed can shift by no more than 1 m/s and that the sensor is never off by more than 0.25 m then the car will never leave the road.
This safety property is not just a property of the neural network, but is instead a temporal property about the model of the entire system, e.g. the car, the road, the physics of the system.
After analysing the system, it turns out that this theorem will be satisfied if the car controller f satisfies the property that if the absolute value of the input sensor readings x1 and x2 are less than 3.25 then the absolute value of f [x1, x2] + 2 * x1 - x2 should be less than 1.25.
We can encode this property in Vehicle as follows:
type InputVector = Tensor Rat [2]
currentSensor = 0
previousSensor = 1
@network
controller : InputVector -> Tensor Rat [1]
safeInput : InputVector -> Bool
safeInput x = forall i . -3.25 <= x ! i <= 3.25
safeOutput : InputVector -> Bool
safeOutput x =
-1.25 < controller x ! 0 + 2 * (x ! currentSensor) - (x ! previousSensor) < 1.25
@property
safe : Bool
safe = forall x . safeInput x => safeOutput x
A neural network controller controller.onnx can be
verified against the specification by running the following command:
vehicle verify \
--specification spec.vcl \
--network controller:controller.onnx \
--verifier Marabou \
--cache controller-resultwhere the last argument tells Vehicle where to write out the result of the verification which will be used by Agda in the next step.
Assuming this property holds, we can export the specification from the cache as follows:
vehicle export \
--target Agda \
--cache controller-result \
--output WindControllerSpec.agdawhich will generate an Agda file:
{-# OPTIONS --allow-exec #-}
open import Vehicle
open import Vehicle.Utils
open import Vehicle.Data.Tensor
open import Data.Product
open import Data.Integer as ℤ using (ℤ)
open import Data.Rational as ℚ using (ℚ)
open import Data.Fin as Fin using (Fin; #_)
open import Data.List.Base
module WindControllerSpec where
InputVector : Set
InputVector = Tensor ℚ (2 ∷ [])
currentSensor : Fin 2
currentSensor = # 0
previousSensor : Fin 2
previousSensor = # 1
postulate controller : InputVector → Tensor ℚ (1 ∷ [])
SafeInput : InputVector → Set
SafeInput x = ∀ i → ℚ.- (ℤ.+ 13 ℚ./ 4) ℚ.≤ x i × x i ℚ.≤ ℤ.+ 13 ℚ./ 4
SafeOutput : InputVector → Set
SafeOutput x = ℚ.- (ℤ.+ 5 ℚ./ 4) ℚ.< (controller x (# 0) ⊕ (ℤ.+ 2 ℚ./ 1) ℚ.* x currentSensor) ⊖ x previousSensor × (controller x (# 0) ⊕ (ℤ.+ 2 ℚ./ 1) ℚ.* x currentSensor) ⊖ x previousSensor ℚ.< ℤ.+ 5 ℚ./ 4
abstract
safe : ∀ x → SafeInput x → SafeOutput x
safe = checkSpecification record
{ verificationFolder = "examples/windController/verificationResult"
}This Agda file can then be imported and used by the larger proof of correctness for the whole system. There is not space to replicate the full proof here, but it can be found here.
6 Conclusions and Future Directions
The tutorial introduced basic concepts in neural network verification, and thereby introduced Vehicle’s architecture:
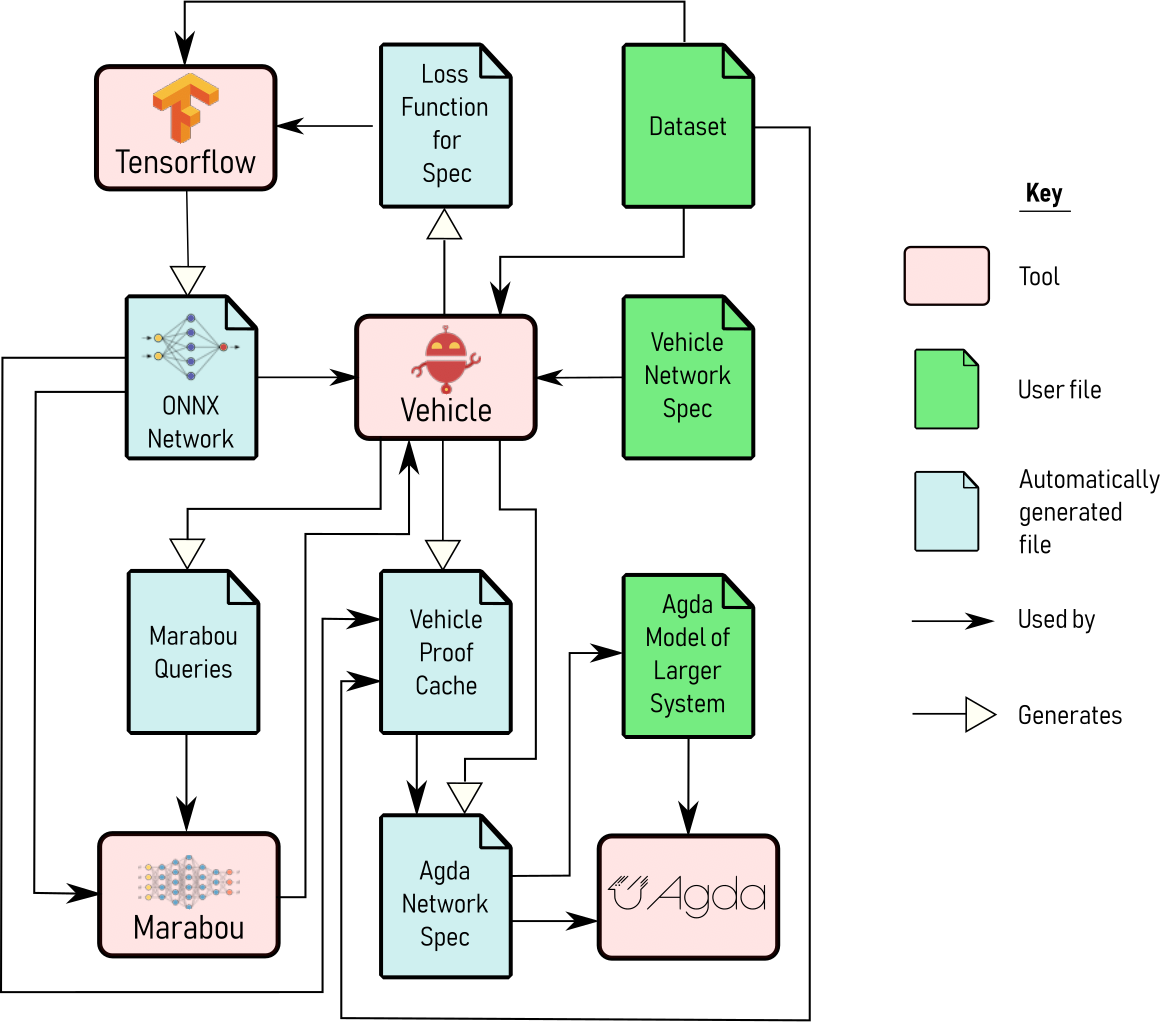
Vehicle is a tool for the whole life-cycle of a neural network verification property:
- Training
- Verification
- Large System Integration
Its possible applications are in proving properties of neural networks applied in different domains:
- Robustness of:
- Intrusion detection systems
- Malware detection systems
- Sanity of physics simulations:
- Monotonicity
- Conservation laws
- Chatbot systems
- Sensor fusion pipelines
- Correctness of control systems:
- Autonomous vehicles
- Network traffic balancing