Introduction

What is Neural Network Verification?

Neural networks are widely used in the field of machine learning; and are often embedded as pattern-recognition or signal processing components into complex software. Below we see a schematic depiction of a neural network trained to classify hand-written digits:

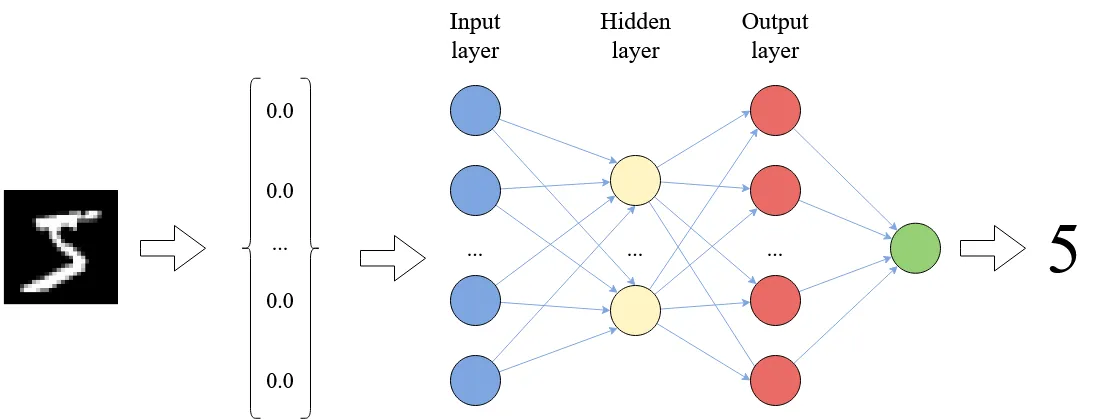
The image is represented as a vector of real numbers, each vector element standing for a pixel value. Each arrow in the picture bears a weight that is used to multiply the input signal; each neuron computes the sum of its inputs.

In some scenarios, it becomes important to establish formal guarantees about neural network behaviour. One of the first known attempts to verify neural networks, by (Pulina & Tacchella, 2010) Pulina, L., & Tacchella, A. (2010). An Abstraction-Refinement Approach to Verification of Artificial Neural Networks. In T. Touili, B. Cook, & P. Jackson (Eds.), Computer Aided Verification (CAV’23) (pp. 243–257). Springer Berlin Heidelberg. , was based on abstract interpretation. The famous paper by Szegedy (Szegedy et al., 2013) Szegedy, C., Zaremba, W., Sutskever, I., Bruna, J., Erhan, D., Goodfellow, I., & Fergus, R. (2013). Intriguing properties of neural networks. International Conference on Learning Representations. http://arxiv.org/abs/1312.6199 that highlighted the problem of neural network vulnerability to small-norm input perturbations (“adversarial attacks”) gave additional impulse to this line of research. In CAV’2017, two papers, by Huang et al (Huang et al., 2017) Huang, X., Kwiatkowska, M., Wang, S., & Wu, M. (2017). Safety Verification of Deep Neural Networks. In R. Majumdar & V. Kuncak (Eds.), Computer Aided Verification - 29th International Conference, CAV 2017, Heidelberg, Germany, July 24-28, 2017, Proceedings, Part I (Vol. 10426, pp. 3–29). Springer. https://doi.org/10.1007/978-3-319-63387-9\_1 and Katz et al. (Katz et al., 2017) Katz, G., Barrett, C., Dill, D. L., Julian, K., & Kochenderfer, M. J. (2017). Reluplex: An efficient SMT solver for verifying deep neural networks. International Conference on Computer Aided Verification, 97–117. , on neural network verification appeared and both used specialised forms of SMT-solving. The later gave rise to Marabou (Katz et al., 2019) Katz, G., Huang, D. A., Ibeling, D., Julian, K., Lazarus, C., Lim, R., Shah, P., Thakoor, S., Wu, H., Zeljić, A., & others. (2019). The Marabou framework for verification and analysis of deep neural networks. International Conference on Computer Aided Verification, 443–452. , a rapidly developing sound and complete neural network verifer, which we use in Vehicle.

In 2019, the ERAN verifier by Dingh et al. (Singh et al., 2019) Singh, G., Gehr, T., Püschel, M., & Vechev, M. (2019). An abstract domain for certifying neural networks. Proceedings of the ACM on Programming Languages, 3(POPL), 1–30. appeared in POPL, and showed that performance of abstract interpretation methods compares favourably against those based on SMT solving. However, the range of properties they handled was limited to proving adversarial robustness of neural networks; moreover ERAN was incomplete. This line of research led to many subsequent extensions, e.g. by Muller et al. (Müller et al., 2022, 2023) Müller, M. N., Fischer, M., Staab, R., & Vechev, M. T. (2023). Abstract Interpretation of Fixpoint Iterators with Applications to Neural Networks. PLDI ’23: 44nd ACM SIGPLAN International Conference on Programming Language Design and Implementation, Orlando, Florida, United States June 17-21, 2023. https://doi.org/10.1145/3591252 Müller, M. N., Makarchuk, G., Singh, G., Püschel, M., & Vechev, M. (2022). PRIMA: general and precise neural network certification via scalable convex hull approximations. Proceedings of the ACM on Programming Languages, 6(POPL), 1–33. to mention a few.

Mixed Integer Linear Programming (MILP) methods were brought into this community by Bastani et al. (Bastani et al., 2016) Bastani, O., Ioannou, Y., Lampropoulos, L., Vytiniotis, D., Nori, A. V., & Criminisi, A. (2016). Measuring Neural Net Robustness with Constraints. In D. D. Lee, M. Sugiyama, U. von Luxburg, I. Guyon, & R. Garnett (Eds.), Advances in Neural Information Processing Systems 29: Annual Conference on Neural Information Processing Systems 2016, December 5-10, 2016, Barcelona, Spain (pp. 2613–2621). https://proceedings.neurips.cc/paper/2016/hash/980ecd059122ce2e50136bda65c25e07-Abstract.html , and were further developed into working tools, e.g. Venus (Botoeva et al., 2020) Botoeva, E., Kouvaros, P., Kronqvist, J., Lomuscio, A., & Misener, R. (2020). Efficient Verification of ReLU-Based Neural Networks via Dependency Analysis. The Thirty-Fourth AAAI Conference on Artificial Intelligence, AAAI 2020, The Thirty-Second Innovative Applications of Artificial Intelligence Conference, IAAI 2020, The Tenth AAAI Symposium on Educational Advances in Artificial Intelligence, EAAI 2020, New York, NY, USA, February 7-12, 2020, 3291–3299. https://ojs.aaai.org/index.php/AAAI/article/view/5729 .

Neural network verifier extensions followed two main directions:

• scaling to larger networks (we can mention -Crown (Wang et al., 2021) Wang, S., Zhang, H., Xu, K., Lin, X., Jana, S., Hsieh, C.-J., & Kolter, J. Z. (2021). Beta-CROWN: Efficient bound propagation with per-neuron split constraints for complete and incomplete neural network verification. Advances in Neural Information Processing Systems, 34. and GCP-Crown (Zhang et al., 2022) Zhang, H., Wang, S., Xu, K., Li, L., Li, B., Jana, S., Hsieh, C.-J., & Kolter, J. Z. (2022). General Cutting Planes for Bound-Propagation-Based Neural Network Verification. Advances in Neural Information Processing Systems. as VNN-COMP winners in 2021 and 2022);

and

• extending from piece-wise linear to non-linear activation functions. (An example are sigmoid neurons handled by Verisig using interval arithmetic (Ivanov et al., 2019) Ivanov, R., Weimer, J., Alur, R., Pappas, G. J., & Lee, I. (2019). Verisig: verifying safety properties of hybrid systems with neural network controllers. In N. Ozay & P. Prabhakar (Eds.), Proceedings of the 22nd ACM International Conference on Hybrid Systems: Computation and Control, HSCC 2019, Montreal, QC, Canada, April 16-18, 2019 (pp. 169–178). ACM. https://doi.org/10.1145/3302504.3311806 .)

At the time of writing, there exist over a hundred verifiers for neural networks. Several papers and monographs are dedicated to the survey of the landscape (e.g., Albarghouthi, 2021; Huang et al., 2020; Liu et al., 2021) Albarghouthi, A. (2021). Introduction to Neural Network Verification. Foundations and Trends® in Programming Languages, 7(1–2), 1–157. https://doi.org/10.1561/2500000051 Huang, X., Kroening, D., Ruan, W., Sharp, J., Sun, Y., Thamo, E., Wu, M., & Yi, X. (2020). A survey of safety and trustworthiness of deep neural networks: Verification, testing, adversarial attack and defence, and interpretability. Comput. Sci. Rev., 37, 100270. https://doi.org/10.1016/j.cosrev.2020.100270 Liu, C., Arnon, T., Lazarus, C., Strong, C. A., Barrett, C. W., & Kochenderfer, M. J. (2021). Algorithms for Verifying Deep Neural Networks. Found. Trends Optim., 4(3–4), 244–404. https://doi.org/10.1561/2400000035 . The community established the specification standards VNNLib, common benchmarks and annual competitions. Vehicle compiles down to the VNNLib standard, with a view to be compatible with the growing family of verifiers.

Formally, a neural network is a function . Verification of such functions most commonly boils down to specifying admissible intervals for the function’s output given an interval for its inputs. For example, one can specify a set of inputs to belong to an - neighborhood of some given input , and verify that for such inputs, the outputs of will be in distance to . This property is often called -ball robustness (or just robustness), as it proves the network’s output is robust (does not change drastically) in the neighborhood of certain inputs.

Seen as functions, neural networks have particular features that play an important role in their verification:

• these functions are not written manually, but generated (or fitted) to model the unknown data distribution;
• the “data” may be big, and require large neural networks;
• we often attribute very little semantic meaning to the resulting function.

Challenges in Neural Network Verification

There are several research challenges in the area of neural network verification:

1. Theory: finding appropriate verification properties. The scope of neural network properties available in the literature is limited. Robustness is the most popular general property to date (Casadio et al., 2021) Casadio, M., Daggitt, M. L., Komendantskaya, E., Kokke, W., Kienitz, D., & Stewart, R. (2021). Property-driven Training: All You (N) Ever Wanted to Know About. arXiv Preprint arXiv:2104.01396. , and others include mostly domain-specific properties, such as ACAS Xu Benchmark (Katz et al., 2017) Katz, G., Barrett, C., Dill, D. L., Julian, K., & Kochenderfer, M. J. (2017). Reluplex: An efficient SMT solver for verifying deep neural networks. International Conference on Computer Aided Verification, 97–117. , which we will consider shortly in this tutorial. What neural network properties we want and can realistically verify still stands as a big research question.

2. Solvers: undecidability of non-linear real arithmetic and scalability of neural network verifiers. On the solver side, undecidability of non-linear real arithmetic (Akbarpour & Paulson, 2009) Akbarpour, B., & Paulson, L. C. (2009). MetiTarski: An Automatic Theorem Prover for Real-Valued Special Functions. Journal of Automated Reasoning, 44(3), 175–205. and scalability of neural network verifiers [wang2021beta] stand as two main challenges.

3. Machine Learning: understanding and integrating property-driven training. In all realistic scenarios, even accurate neural networks require extra “property-driven training” in order to comply with verification properties in question. This requires new methods of integrating training with verification. Several approaches exist, including the recently introduced method of “differentiable logics” that translate logical properties into loss functions. But they all have pitfalls, see (Slusarz et al., 2023) Slusarz, N., Komendantskaya, E., Daggitt, M. L., Stewart, R. J., & Stark, K. (2023). Logic of Differentiable Logics: Towards a Uniform Semantics of DL. In R. Piskac & A. Voronkov (Eds.), LPAR 2023: Proceedings of 24th International Conference on Logic for Programming, Artificial Intelligence and Reasoning, Manizales, Colombia, 4-9th June 2023 (Vol. 94, pp. 473–493). EasyChair. https://doi.org/10.29007/c1nt for a discussion.

4. Programming: finding the right languages to support these developments Many existing solvers have low-level syntax that is hard to understand, making maintenance of the specification difficult. There is very little programming infrastructure to interface verification and property-driven training. Furthermore, the available language infrastructure only allows specifications to be written in terms of the input space, whereas one often needs to reason about neural network behavior in terms of the problem space. This creates an additional embedding gap on verification side, a problem that eventually needs to be resolved.

5. Complex systems: integration of neural net verification into complex systems. Finally, neural networks usually work as components of complex systems, and the question of smooth integation of existing neural network solvers with other theorem provers requires resolution.

This tutorial will focus on problems 3 to 5, and will present Vehicle, a tool that provides support in alleviating them. In particular, Vehicle is equipped with a specification language that allows one to express neural network properties in a high-level, human-readable format (thus opening the way to reasoning about a wider space of properties, and reasoning in terms of the problem space). Then it compiles the specification down into low-level queries and passes them automatically to existing neural network solvers. If the specification cannot be verified, Vehicle gives one an option to automatically generate a new loss function that can be used to train the model to satisfy the stated property. Once a specification has been verified (possibly after property-driven re-training), Vehicle allows one to export the proof to an interactive theorem prover, and reason about the behavior of the complex system that embeds the machine learning model.

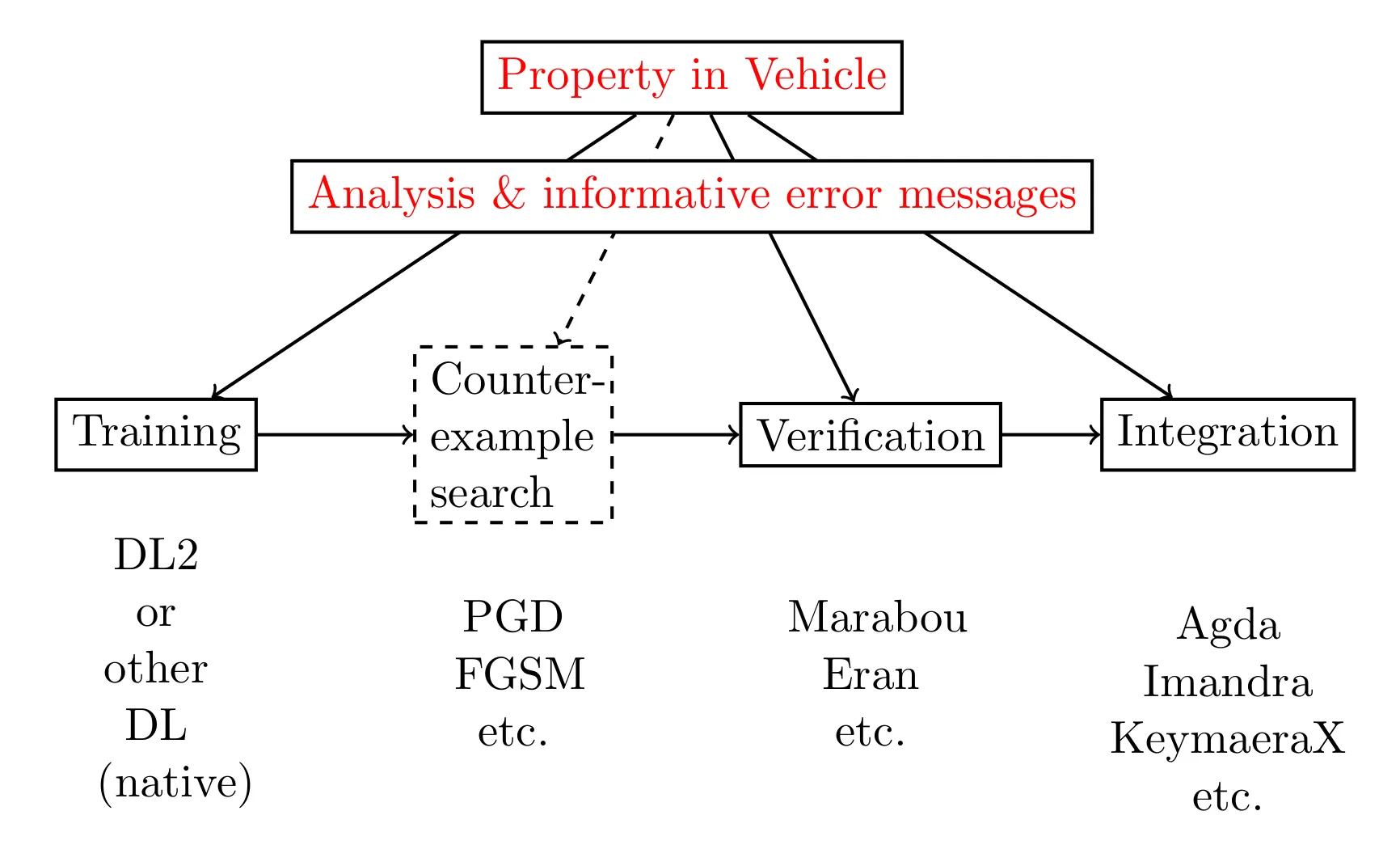
Vehicle programs can be compiled to an unusually broad set of backends, including:

a) loss functions for Tensorflow which can be used to guide both specification-directed training and gradient-based counter-example search.

b) queries for the Marabou neural network verifier, which can be used to formally prove that the network obeys the specification.

c) Agda specifications, which are tightly coupled to the original network and verification result, in order to scalably and maintainably construct larger proofs about machine learning-enhanced systems.

Currently, Vehicle supports the verifier Marabou, the ITP Agda, and the ONNX format for neural networks. The below figure illustrates the existing user backends in Vehicle.

Objectives of this Tutorial

This tutorial will give an introduction to the Vehicle tool and its conceptual approach to modelling specifications for machine learning systems via functional programming. It will teach the participants to understand the range of problems that arise in neural network property specification, verification and training, and will give hands-on experience at solving these problems at a level of a higher-order specification language with dependent types.

Prerequisites

To follow the tutorial, you will need Vehicle, Marabou and Agda installed in your machine. For instructions, refer to vehicle documentation.

Quick installation instructions:

• For Chapters 1, 2 and 3 you only need to

  1. Install Vehicle : just run pip install vehicle-lang

  2. Install Marabou: just run pip install maraboupy

• Python (Tensorflow) and Agda installation will only be needed to follow Chapters 4 and 5.

We suggest that you start this tutorial with just Vehicle and Marabou as tools.

We recommend using Visual Studio Code with the Vehicle Syntax Highlighting and agda-mode plugins.

Whether you are using this tutorial for self-study or attending one of our live tutorials, all supporting exercises, code and infrastructure can be downloaded from the tutorial repository. These include all relevant property specifications, trained neural networks in ONNX format, data in IDX format, and any necessary instructions.

Further Reading

If you are interested to know more about the theoretical underpinnings of Vehicle design, we recommend the following papers:

• Daggitt, M.L., Kokke. W., Atkey, R., Slusarz, N., Arnaboldi, L., Komendantskaya, E.: Vehicle: Bridging the Embedding Gap in the Verification of Neuro-Symbolic Programs. arXiv, 2024.

• Casadio, M., Komendantskaya, E., Daggitt, M.L., Kokke, W., Katz, G., Amir, G., Refaeli, I.: Neural network robustness as a verification property: A principled case study. In: Shoham, S., Vizel, Y. (eds.) Computer Aided Verification - 34th International Conference, CAV 2022, Haifa, Israel, August 7-10, 2022, Proceedings, Part I. Lecture Notes in Computer Science, vol. 13371, pp. 219–231. Springer (2022)

• Daggitt, M.L., Atkey, R., Kokke, W., Komendantskaya, E., Arnaboldi, L.: Compiling higher-order specifications to SMT solvers: How to deal with rejection constructively. In: Krebbers, R., Traytel, D., Pientka, B., Zdancewic, S. (eds.) Proceedings of the 12th ACM SIGPLAN International Conference on Certified Programs and Proofs, CPP 2023, Boston, MA, USA, January 16-17, 2023. pp. 102–120. ACM (2023).

• Slusarz, N., Komendantskaya, E., Daggitt, M.L., Stewart, R.J., Stark, K.: Logic of Differentiable Logics: Towards a Uniform Semantics of DL. LPAR 2023. Proceedings of 24th International Conference on Logic for Programming, Artificial Intelligence and Reasoning, Manizales, Colombia, 4-9th June 2023, EPiC Series in Computing, vol. 94, pp. 473–493.