Property-Driven Training

Motivation

We finished the last chapter with a conjecture concerning diminishing robustness verification success with increasing values of . Let us now see, using a concrete example, how soon the success rate declines.

The last exercise of the previous chapter gave us a property specification for robustness of “Fashion MNIST” models. We propose now to look into the statistics of verifying one of such models on 500 examples from the data set. To obtain quicker verification times, let us use a Fashion MNIST model with one input layer of neurons, and one output layer of neurons (the tutorial files contain the model if you wish to check it). Running Vehicle, we obtain the following success rates:

As we see in the table, verifiability of the property deteriorates quickly with growing . Yet, for majority of practical applications, it is desirable to have a larger , as this increases the chance that new yet unseen data points will fall within the verified subspaces of the input vector space.

Can we re-train the neural network to be more robust within a desirable ? The long tradition of robustifying neural networks in machine learning has a few methods ready, for example, to re-train the networks with new data set that was augmented with images within the desired -balls, or to generate adversarial examples (sample images closest to the decision boundary) within the given -balls during training.

Let us look closer into this.

Robustness Training

Data Augmentation

Suppose we are given a data set . Prior to training, we can generate new training data samples within -balls of the existing data and label them with the same output as the original data. Then we can use our usual training methods with this new augmented data set (Shorten & Khoshgoftaar, 2019) Shorten, C., & Khoshgoftaar, T. M. (2019). A survey on image data augmentation for deep learning. J. Big Data, 6(60). .

However, this method maybe problematic for verification purposes. Let us have a look at its effect, pictorially. Suppose this is the manifold that corresponds to (crosses are the original data points, and circles are the -balls around them):

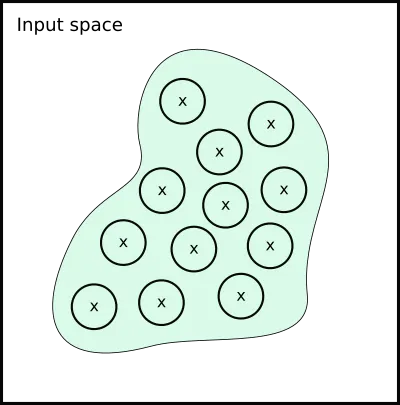
Remember that we sampled our new data from these -balls. But suppose your true decision boundary runs over the manifold like this:

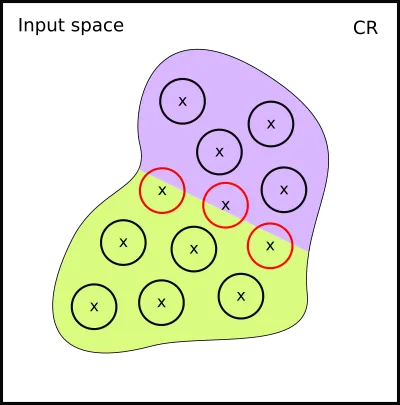
We have a problem, because some of the data points we sampled from the suddenly have wrong labels!

Actually, it maybe even worse. Depending how our data lies on the manifold, we may have even generated inconistent labelling. Here is the example when this happens:

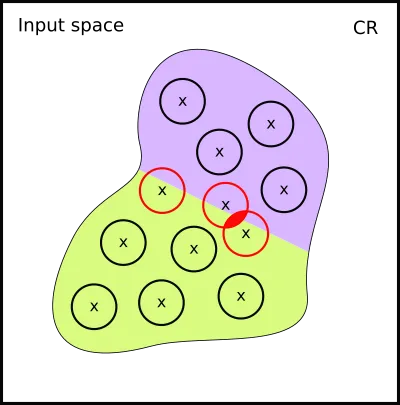
It seems data augmentation is not general enough for Vehicle, and only works correctly if strong assumptions about the underlying manifold are taken.

Adversarial Training

It would be nice to somehow reflect the fact of proximity to the decision boundary in our training! The closer the point is to the decision boundary, the less certain the neural network should be about its class:

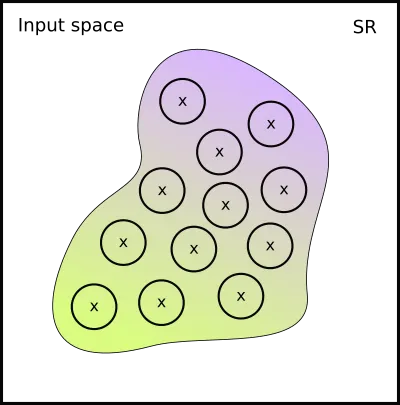
However, using data labels as a method is unfit for the task. We cannot achieve the effect we are looking for with data augmentation. We have to modify our training algorithm instead (Goodfellow et al., 2015) Goodfellow, I. J., Shlens, J., & Szegedy, C. (2015). Explaining and Harnessing Adversarial Examples. In Y. Bengio & Y. LeCun (Eds.), 3rd International Conference on Learning Representations, ICLR 2015, San Diego, CA, USA, May 7-9, 2015, Conference Track Proceedings. .

Loss Function

Given a data set and a function with optimisation parameters , a loss function

computes a penalty proportional to the difference between the output of on a training input and a desired output .

The reader will find an excellent exposition of adversarial training in the tutorial by Kolter & Madry (2018) Kolter, Z., & Madry, A. (2018). Adversarial Robustness - Theory and Practice. In NeurIPS 2018 tutorial. .

Example: Cross-Entropy Loss

Given a function , the cross-entropy loss is defined as

where is the true probability for class and is the probability for class as predicted by when applied to .

Adversarial Training for Robustness

Gradient descent minimises loss between the predicted value and the true value , for each entry in . It thus solves the optimisation problem:

For adversarial training, we instead minimise the loss with respect to the worst-case perturbation of each sample in . We replace the standard training objective with:

The inner maximisation is done by projected gradient descent (PGD), that “projects” the gradient of on in order to perturb it and get the worst .

Adversarial Training and Verification

Adversarial training is almost the right solution! Its main limitation turns out to be the logical property it optimises for. Recall that we may encode an arbitrary property in Vehicle. However, as we discovered in (Casadio et al., 2022) Casadio, M., Komendantskaya, E., Daggitt, M. L., Kokke, W., Katz, G., Amir, G., & Refaeli, I. (2022). Neural Network Robustness as a Verification Property: A Principled Case Study. In S. Shoham & Y. Vizel (Eds.), Computer Aided Verification - 34th International Conference, CAV 2022, Haifa, Israel, August 7-10, 2022, Proceedings, Part I (Vol. 13371, pp. 219–231). Springer. https://doi.org/10.1007/978-3-031-13185-1\_11 , the projected gradient descent can only optimise for one concrete property. Recall the property of -ball robustness was defined as: . It turns out that adversarial training determines the definition of robust to be .

Logical Loss Functions

The main idea is that we would like to co-opt the same gradient-descent algorithm that is used to train the network to fit the data to also train the network to obey the specification.

Logical Loss Function: Simple Example

Consider the very simple example specification:

@network
f : Tensor Real [1] -> Tensor Real [1]

@property
greaterThan2 : Bool
greaterThan2 = f [ 0 ] ! 0 > 2

This statement is either true or false, as shown in the left graph below:

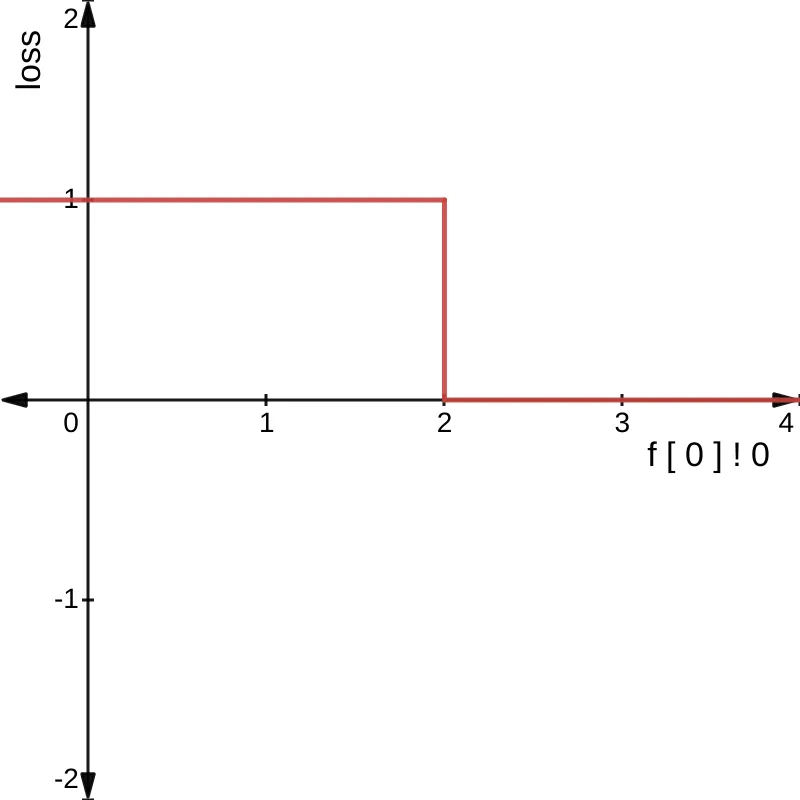
However, what if instead, we converted all Bool values to Real, where a value greater than 0 indicated false and a value less than 0 indicated true? We could then rewrite the specification as:

greaterThan2 : Real
greaterThan2 = f [ 0 ] ! 0 - 2

If we then replot the graph we get the following:

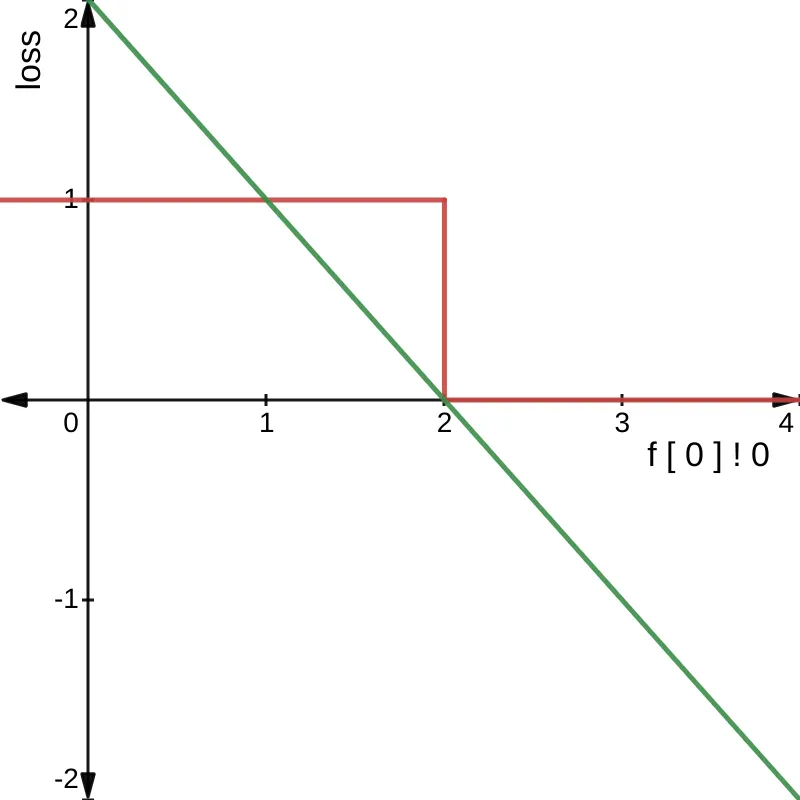
Now we have a useful gradient, as successfully minimising f [ 0 ] ! 0 - 2 will result in the property greaterThan2 becoming true.

This is the essence of logical loss functions: convert all booleans and operations over booleans into equivalent numeric operations that are differentiable and whose gradient’s point in the right direction.

Differentiable Logics

Traditionally, translations from a given logical syntax to a loss function are known as “differentiable logics”, or DLs. One of the first attempts to translate propositional logic specifications to loss functions was given in (Xu et al., 2018) Xu, J., Zhang, Z., Friedman, T., Liang, Y., & den Broeck, G. V. (2018). A Semantic Loss Function for Deep Learning with Symbolic Knowledge. In J. G. Dy & A. Krause (Eds.), Proceedings of the 35th International Conference on Machine Learning, ICML 2018, Stockholmsmässan, Stockholm, Sweden, July 10-15, 2018 (Vol. 80, pp. 5498–5507). PMLR. http://proceedings.mlr.press/v80/xu18h.html and was generalised to a fragment of first-order logic in (Fischer et al., 2019) Fischer, M., Balunovic, M., Drachsler-Cohen, D., Gehr, T., Zhang, C., & Vechev, M. T. (2019). DL2: Training and Querying Neural Networks with Logic. In K. Chaudhuri & R. Salakhutdinov (Eds.), Proceedings of the 36th International Conference on Machine Learning, ICML 2019, 9-15 June 2019, Long Beach, California, USA (Vol. 97, pp. 1931–1941). PMLR. http://proceedings.mlr.press/v97/fischer19a.html . Later, this work was complemented by giving a fuzzy interpretation to DL by (van Krieken et al., 2022) van Krieken, E., Acar, E., & van Harmelen, F. (2022). Analyzing Differentiable Fuzzy Logic Operators. Artif. Intell., 302, 103602. https://doi.org/10.1016/j.artint.2021.103602 and (Slusarz et al., 2023) Slusarz, N., Komendantskaya, E., Daggitt, M. L., Stewart, R. J., & Stark, K. (2023). Logic of Differentiable Logics: Towards a Uniform Semantics of DL. In R. Piskac & A. Voronkov (Eds.), LPAR 2023: Proceedings of 24th International Conference on Logic for Programming, Artificial Intelligence and Reasoning, Manizales, Colombia, 4-9th June 2023 (Vol. 94, pp. 473–493). EasyChair. https://doi.org/10.29007/c1nt proposed generalisation for the syntax and semantics of DL, with a view of encoding all previously presented DLs in one formal system, and comparing their theoretical properties.

Vehicle has several different differentiable logics from the literature available, but will not go into detail about how they work here.

Instead, we explain the main idea by means of an example. Let us define a very simple differentiable logic on a toy language

One possible DL (called Product DL in (van Krieken et al., 2022) van Krieken, E., Acar, E., & van Harmelen, F. (2022). Analyzing Differentiable Fuzzy Logic Operators. Artif. Intell., 302, 103602. https://doi.org/10.1016/j.artint.2021.103602 ) for it can be defined as:

An example of this translation is:

Logical Loss Functions in Vehicle

We now have all the necessary building blocks to define Vehicle approach to property-driven training. We use the formula:

In Vehicle, given a property , we replace the usual PGD training objective with

where

• is a hyper-shape that corresponds to the pre-condition and
• is obtained by DL-translation of the post-condition .

Let us see how this works for the following definition of robustness:

The definition of the optimisation problem above instantiates by taking:

• given by the -cube around and
• given any DL translation , the loss function

Coding Example: generating a logical loss function in Python

The Python bindings ship backend-specific helpers in vehicle_lang.loss.tensorflow and vehicle_lang.loss.pytorch. They both expose a single entry point load_specification(path, ...) which compiles your .vcl file to a dictionary of callable Python loss functions. The returned dictionary keys are the names of @property declarations in your spec.

Below is a minimal PyTorch example that mirrors the tests in vehicle-python/tests:

import torch
from vehicle_lang.typing import DifferentiableLogic
from vehicle_lang.loss.pytorch import load_specification

# Compile the Vehicle spec to PyTorch loss functions
spec = load_specification(
    "test_trainable.vcl",  # any Vehicle spec path
    logic=DifferentiableLogic.Vehicle,
)

constraint_loss = spec["output_bounded"]  # name of a @property in the spec

train_x = torch.tensor([0.0, 0.5, 1.0], dtype=torch.float32).unsqueeze(1)
train_y = torch.tensor([0.0, 1.0, 2.0], dtype=torch.float32)

model = torch.nn.Sequential(
    torch.nn.Linear(1, 8), torch.nn.ReLU(), torch.nn.Linear(8, 1)
)
optimizer = torch.optim.Adam(model.parameters(), lr=1e-2)

for step in range(50):
    optimizer.zero_grad()

    # Task loss (e.g., MSE to a target function)
    preds = model(train_x).squeeze(1)
    task_loss = torch.mean((preds - train_y) ** 2)

    # Constraint loss produced by Vehicle; signature matches the Vehicle property
    constraint_loss_value = constraint_loss(model)

    loss = 0.5 * task_loss + 0.5 * constraint_loss_value
    loss.backward()
    optimizer.step()

Switching to TensorFlow changes only the backend import and model definition; the property call still follows the spec’s argument list (typically a single network callable for many specs):

import tensorflow as tf
from vehicle_lang.typing import DifferentiableLogic
from vehicle_lang.loss.tensorflow import load_specification

spec = load_specification("test_trainable.vcl", logic=DifferentiableLogic.Vehicle)
constraint_loss = spec["output_bounded"]

train_x = tf.constant([[0.0], [0.5], [1.0]], dtype=tf.float32)
train_y = tf.constant([0.0, 1.0, 2.0], dtype=tf.float32)

model = tf.keras.Sequential([
    tf.keras.layers.Input(shape=(1,)),
    tf.keras.layers.Dense(8, activation="relu"),
    tf.keras.layers.Dense(1),
])

optimizer = tf.keras.optimizers.Adam(learning_rate=1e-2)

for step in range(50):
    with tf.GradientTape() as tape:
        preds = tf.squeeze(model(train_x), axis=1)
        task_loss = tf.reduce_mean(tf.square(preds - train_y))

        constraint_loss_value = constraint_loss(model)
        loss = 0.5 * task_loss + 0.5 * constraint_loss_value

    grads = tape.gradient(loss, model.trainable_variables)
    optimizer.apply_gradients(zip(grads, model.trainable_variables))

Optional parameters such as logicand samplers are available on load_specification; see the Python API docs for defaults and examples. To customise how Vehicle searches adversarial points, you can supply your own sampler (cf. the default FGSM-based samplers in the source tree) when you have domain-specific needs.