Proving Neural Network Robustness

Neural Network Robustness as a Verification Property

In this chapter we will learn about the problem that has received significant attention within the machine learning community: the problem of robustness of neural networks to out-of-distribution shifts, also known as “robustness to adversarial attacks”. The problem was famously raised by Christian Szegedy and his co-authors in 2013 in the paper “Intriguing properties of neural networks”

So, here is the problem. Suppose we are given a data set for classification of images, it consists of pairs , where is an input, and is the desired output. It is assumed that the outputs are generated from by some function and that is drawn from some probability distribution over .

Let us take as an example the famous MNIST data set by LeCun et al. The images look like this:

As we have already discussed in the previous chapter, a neural network is a function parametrised by a set of weights . The goal of training is to use the dataset to find weights such that approximates well over input regions with high probability density.

When we train a neural network to be highly accurate on both the training and the test sets, we emprically test:

• how well the neural network can in principle approximate (we do this by measuring its accuracy on the training set);
• how well that learnt hypothesis generalises to yet unseen data (we do this by measuring the accuracy on the test set).

Coming to our example, if my neural network has a % accuracy on the MNIST data set, I should be satisfied that it learnt what a hand-written digit is. Szegedy et al were the first to show systematically that this is not the case: take the image on the left (below), which is classified with high confidence as “0”, apply perturbation on the middle to get the image on the right, and your neural network will give a % confidence that it sees a “5” on the right, even despite the fact that the image did not change the class (for the human eye):

Original MNIST Image	Perturbation	Resulting Perturbed Image

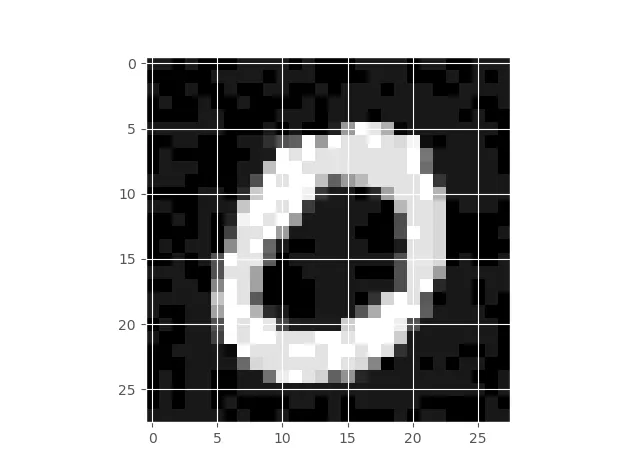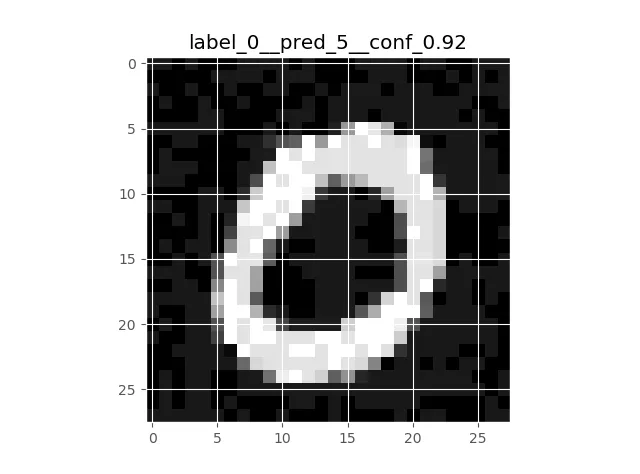This experiment can be replicated for any data set and any neural network, no matter how accurate it is.

The root of the problem is: the image on the right no longer belongs to the probability distribution that the network has learnt (whether or not the image looks the same to a human observer). We could phrase it differently: an ideal probability distribiution that is “learnt” by a “human” accounts not only for the images we obtained as part of the dataset , but also involves an implicit assumption that “semantically” similar images belong to the same class.

The simplest way to capture this implicit assumption is to formulate a verification property that insists that all similar images (images within an distance of each other in ) are classified similarly. This property is often called -ball robusness. For every image in the dataset, we assume we can “draw” a small -ball around it, and guarantee that within that -ball classification of the network does not change much (the ball’s radius below is given by the chosen ):

-ball around a number “7” in MNIST

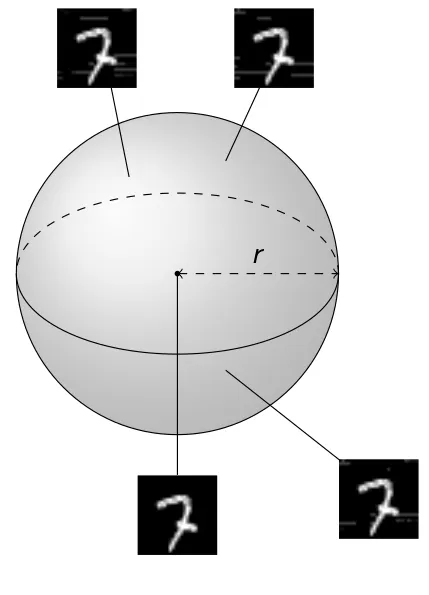Formally, we define an -ball around an image as:

where is a distance function (or -norm) in , such as Euclidean distance or -norm.

It now remains to define the property “classification of does not change much”. The paper by Casadio et al. summarises a few options for this definition. The simplest is the Classification Robustness that requires that all images within any given -ball are classified as the same class. We will consider this property in detail, and will take a few other properties from Casadio et al. as an exercise.

Formalising -ball robustness for MNIST networks in Vehicle

We note that -ball robustness as a verification property bears some similarity to the ACAS Xu example that we have already covered in Chapter 1. In particular, both verification properties impose constraints on the output regions of the neural networks, assuming some constraint on their input regions. (Both problems are therefore amenable to a range of interval propagation and abstract interpretation methods, see this survey for further details.) From the point of view of the property specification, which is our main concern here, there are three main differences between these two examples:

• ACAS Xu did not have to refer to a dataset ; -ball robustness, however, is formulated relative to the images given in the data set. We will see how Vehicle can be used to handle properties that refer directly to the data sets.

• MNIST, as many other data sets used in Computer Vision, has images represented as 2D arrays. Such data sets often require Convolutional Neural Networks (CNNs) that are best designed to deal with 2D and 3D data. In terms of property specification, we will see Vehicle’s support for 2D arrays, which comes for free with its general type infrastructure.

• Finally, the MNIST specification involves two parameters that we may want to pass or infer at the compilation time rather than hard-code within the spec. These are the and the number of data points (-balls) we wish to check (the number is at most the size of the entire data set). We will see how such parameters are defined and used in Vehicle.

2D Arrays in Vehicle

Starting a specification for MNIST data set follows the same pattern as we have seen in Chapter 1, only this time we declare inputs as 2D arrays:

type Image = Tensor Real [28, 28]
type Label = Index 10

As before, we define valid inputs, this time making a mild adaptation to 2D arrays and assuming all pixel values are normalised between 0 and 1:

validImage : Image -> Bool
validImage x = forall i j . 0 <= x ! i ! j <= 1

The output of the network is a score for each of the digits 0 to 9.

@network
classifier : Image -> Tensor Real [10]

We note again the use of the syntax for @network, marking the place where Vehicle interacts with an external tool (this time most likely with Python Tensorflow).

The classifier advises that input image x has label i if the score for label i is greater than the score of any other label j:

advises : Image -> Label -> Bool
advises x i = forall j . j != i => classifier x ! i > classifier x ! j

This completes the basic description if the data set and the model architecture in Vehicle. We are ready to define verification properties.

Definition of Robustness Around a Point

First we define the parameter epsilon that will represent the radius of the balls that we verify. Note that we declare this as a parameter which allows the value of epsilon to be specified at compile time rather than be fixed in the specification. We again use the syntax @ to communicate this information externally:

@parameter
epsilon : Real

Next we define what it means for an image x to be in a ball of size epsilon. The definition below uses the norm, defined as:

where computes the maximum element of . Below, we shortcut a bit the calculation of being bounded by and simply require that all vector elements are bounded by :

boundedByEpsilon : Image -> Bool
boundedByEpsilon x = forall i j . -epsilon <= x ! i ! j <= epsilon

Using the Eucledian distance would require a slightly more complicated definition, which we will do as an exercise.

We now define what it means for the network to be robust around an image x that should be classified as y. Namely, we define that for any perturbation no greater than , if the perturbed image is still a valid image then the network should still advise label y for the perturbed version of x.

robustAround : Image -> Label -> Bool
robustAround image label = forall pertubation .
  let perturbedImage = image - pertubation in
  boundedByEpsilon pertubation and validImage perturbedImage =>
    advises perturbedImage label

Again, note the use of a quantifier forall that ranges over an infinite domain of images of type Image.

Definition of Robustness with Respect to a Dataset

We first specify parameter n , which stands for the size of the training dataset. Unlike the earlier parameter epsilon, we set the infer option of the parameter n to ‘True’. This means that it does not need to be provided manually but instead will be automatically inferred by the compiler. In this case it will be inferred from the training datasets.

@parameter(infer=True)
n : Nat

We next declare two datasets, the training images and the corresponding training labels. Note that we use the previously declared parameter n to enforce that they are of the same size:

@dataset
trainingImages : Vector Image n

@dataset
trainingLabels : Vector Label n

Again we note the use of syntax that involves @ flagging Vehicle’s connection with an external tool or object – in this case, the data set is defined externally.

We then say that the network is robust for this data set if it is robust around every pair of input images and output labels. Note once again the use of the foreach keyword when quantifying over the index i in the dataset. Whereas forall would return a single Bool, foreach constructs a Vector of booleans, ensuring that Vehicle will report on the verification status of each image in the dataset separately. If forall was omitted, Vehicle would only report if the network was robust around every image in the dataset, a state of affairs which is unlikely to be true.

@property
robust : Vector Bool n
robust = foreach i . robustAround (trainingImages ! i) (trainingLabels ! i)

Running the Verification Query

In order to run Vehicle, we need to provide:

• the specification file,
• the network in ONNX format,
• the data in idx format,
• and the desired value.

The tutorial files contain two Python scripts that show how to convert Tensorflow Neural Networks into ONNX format; and images – into .idx files. These are the formats expected by Vehicle. You can use the ones we provide, or generate your own. Having obtained these, the following command line will take care of verification of the network mnist-classifier.onnx, for data sets images.idx and labels.idx and :

vehicle verify \
  --specification mnist-robustness.vcl \
  --network classifier:mnist-classifier.onnx \
  --parameter epsilon:0.005 \
  --dataset trainingImages:t2-images.idx \
  --dataset trainingLabels:t2-labels.idx \
  --verifier Marabou

For the first two images in your data set, the output will look as follows:

Verifying properties:
  robust [================================================] 9/9 queries complete
  robust [================================================] 9/9 queries complete
Result: true
  robust: 2/2 verified
    ✓ robust!0

    ✓ robust!1

The reader may have guessed at this pont that, as we make larger, fewer and fewer examples will staisfy the property. Chapter 3 will look into methods that can be used to train networks to satisfy robustness for larger .

Exercises

Exercise (⭑): Run the Chapter code

As usual, your first task is to repeat the steps described in this chapter: download the Vehicle specification, the network, the data, and verify robustness of the given network on given data. All code is available from the examples section of the tutorial repository

Exercise (⭑) : Experimenting with -balls of different size

Try experimenting with different values of , for example, try . Make conclusions.

Exercise (⭑⭑) : Getting a statistical evaluation of robustness with respect to the given data set, for various s

(This exercise is technically very simple, but the required number of experiments may take a few hours to run. We recommend you run it at home rather than during the live exercise sessions).

The previous exercise could be transformed into a proper empirical evaluation of robustness of the model for the data set. To do this, include more than 2 images into your idx file. A script for generating idx files is available in the supporting materials.

Assuming you created an idx file with, for example, 500 images, run Vehicle on this file, and collect statistics for . You should be able to populate a table that looks like this:

This is your first proper empirical evaluation of the given neural network for the given data set! This kind of evaluation is reported in international competitoions such as VNNComp and in research papers.

Make conclusion about feasibility and success rates of -ball robustness, and the speed with which verification success deteriorates with the growing .

Exercise (⭑) : Strong Classification Robustness in Vehicle

Using the same .vcl file as in all previous exercises, define and verify in Vehicle the propety of Strong Classification Robustness, that requires, for all in the -ball of , that , for some small . We now assemble the desired_strong classification robustness_ property definition:

Given an ,

We refer the interested reader for a more detailed discussion of different robustness properties in:

• Marco Casadio, Ekaterina Komendantskaya, Matthew L. Daggitt, Wen Kokke, Guy Katz, Guy Amir, Idan Refaeli: Neural Network Robustness as a Verification Property: A Principled Case Study. CAV (1) 2022: 219-231.

• Xiaowei Huang, Daniel Kroening, Wenjie Ruan, James Sharp, Youcheng Sun, Emese Thamo, Min Wu, Xinping Yi. A Survey of Safety and Trustworthiness of Deep Neural Networks: Verification, Testing, Adversarial Attack and Defence, and Interpretability. J. of Computer Science Review, 2018.

Exercise (⭑⭑): Explore Other Definitions of Robustness

Use Vehicle to define other forms of Robustness property from Casadio et al.

Please note: although the Vehicle language is rich enough to compile all the robustness definitions, not all definitions will be feasible for Marabou that can have only one occurence of a neural network per specification.

Exercise (⭑⭑): Other Distances in Vehicle

Re-define the classification and standard robustness properties by using some different notion of distance, e.g. the Euclidean distance, instead of the norm.

Please note: although the Vehicle language is rich and allows such extensions, not all specifications will be feasible for Marabou that works with linear real arithmetic.

Exercise (⭑) Practicing to write property specifications

To test your understanding of the robustness property, try completing the robustness verification in this file.

Exercise (⭑⭑⭑): Conduct a complete “training - verification” experiment from start to finish

This exercise can be hard or simple, depending how much help you get from the model solution provided as sources!

We will work with the Fashion MNIST data set.

Either:

• download the data set, train a model from scratch, generate onnx and idx files; or
• obtain the model and idx files directly from the directory with the supporting materials

Once this is done, define the spec and verify its robustness. Experiment with different values of and different definitions of robustness.